Feladat:	Gy.3149	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Deli Lajos ,  Pótó Júlia ,  Szilasi Zoltán ,  Szűcs Zsófia ,  Tokodi Tünde
Füzet:	1998/március, 151 - 152. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek egybevágósága, Pitagorasz-tétel alkalmazásai, Elsőfokú (és arra visszavezethető) egyenletrendszerek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/szeptember: Gy.3149

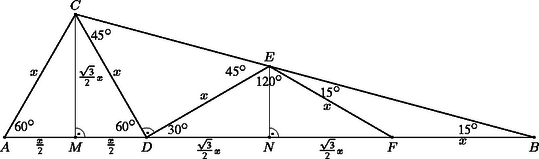
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Válasszuk a háromszög csúcsainak jelölését úgy, hogy az $A$-nál lévő szög legyen ${60}^{\circ }$-os, a $B$-nél lévő pedig ${15}^{\circ }$-os. Ekkor a $C$-nél lévő szög ${180}^{\circ }-\left({60}^{\circ }+{15}^{\circ }\right)={105}^{\circ }$. Vegyük fel az $AB$ oldalon a $D$ pontot úgy, hogy $ACD\sphericalangle ={60}^{\circ }$ legyen, majd a $BC$ oldalon az $E$ pontot úgy, hogy $CDE\sphericalangle ={90}^{\circ }$ legyen, végül az $AB$ oldalon az $F$ pontot úgy, hogy $DEF\sphericalangle ={120}^{\circ }$ legyen (1. ábra). Ekkor egyszerű számolással meghatározhatjuk az $ACD$, $CDE$, $DEF$ és $EFB$ háromszögek szögeit: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle ADC\sphericalangle }& {\displaystyle ={180}^{\circ }-\left(DAC\sphericalangle +ACD\sphericalangle \right)={60}^{\circ };}\hfill \\ \hfill {\displaystyle DCE\sphericalangle }& {\displaystyle =ACB\sphericalangle -ACD\sphericalangle ={45}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle DEC\sphericalangle }& {\displaystyle ={180}^{\circ }-\left(CDE\sphericalangle +DCE\sphericalangle \right)={45}^{\circ };}\hfill \\ \hfill {\displaystyle EDF\sphericalangle }& {\displaystyle ={180}^{\circ }-ADE\sphericalangle ={30}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle DFE\sphericalangle }& {\displaystyle ={180}^{\circ }-\left(EDF\sphericalangle +DEF\sphericalangle \right)={30}^{\circ };}\hfill \\ \hfill {\displaystyle EFB\sphericalangle }& {\displaystyle ={180}^{\circ }-EFA\sphericalangle ={150}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle FEB\sphericalangle }& {\displaystyle ={180}^{\circ }-CEF\sphericalangle ={15}^{\circ }\mathrm{.}}\hfill \end{array}}}\end{array}$ Tehát az $ACD$ háromszög szabályos, a $CDE$, $DEF$ és $EFB$ háromszögek pedig egyenlő szárúak. Ha $AC$ hosszát $x$-szel jelöljük, akkor $AC=AD=CD=DE=EF=FB=x$. Legyen $AD$ felezőpontja $M$, $DF$ felezőpontja pedig $N$. Mivel az $ADC$ háromszög szabályos, ezért $CM$ merőleges $AD$-re, $AM=MD=\frac{x}{2}$ és $CM=\frac{\sqrt[]{3}}{2}\cdot x$. Az $EN$ szakasz is merőleges $DF$-re, ezért a $CMD$ és a $DNE$ háromszögek megfelelő szögei megegyeznek. Mivel $CD=DE$ is teljesül, ezért a két háromszög egybevágó, vagyis $DN=CM=\frac{\sqrt[]{3}}{2}\cdot x$, és mivel $N$ a $DF$ felezőpontja, ezért $FN=DN=\frac{\sqrt[]{3}}{2}\cdot x$. Ezeket felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle 1=AB=AD+DN+NF+FB=x+\frac{\sqrt[]{3}}{2}\cdot x+\frac{\sqrt[]{3}}{2}\cdot x+x=\left(2+\sqrt[]{3}\right)x\mathrm{.}}\end{array}$ Vagyis $x=\frac{1}{2+\sqrt[]{3}}=2-\sqrt[]{3}$. A $BC$ oldal hosszát a $BCM$ derékszögű háromszögből határozhatjuk meg Pitagorasz tételét felhasználva: $\begin{array}{c}{\displaystyle B{C}^2=C{M}^2+M{B}^2={\left(\frac{\sqrt[]{3}}{2}\cdot x\right)}^2+{\left(1-\frac{x}{2}\right)}^2=x^2-x+1=6-3\sqrt[]{3}\mathrm{.}}\end{array}$ Tehát az $ABC$ háromszög másik két oldalának hossza $2-\sqrt[]{3}$ és $\sqrt[]{6-3\sqrt[]{3}}$.  Pótó Júlia (Budapest, Veres P. Gimn., 9. évf.)   II. Megoldás. Feltehetjük, hogy az $ABC$ háromszögben az $A$-nál lévő szög ${60}^{\circ }$-os, a $B$-nél lévő pedig ${15}^{\circ }$-os. A háromszög $C$-nél lévő szöge tompaszög, ezért a $B$-ből induló magasság $T$ talppontja az $AC$ oldal $C$-n túli meghosszabbításán van (2. ábra). Legyen $AC=x$ és $CT=y$. Mivel $BAT\sphericalangle ={60}^{\circ }$ és $ATB\sphericalangle ={90}^{\circ }$, ezért $ABT\sphericalangle ={30}^{\circ }$, a $BAT$ háromszöget a $BT$ egyenesre tükrözve a tükörkép és az eredeti háromszög együtt egy szabályos háromszöget alkot, melynek oldalhossza $AB=1$. Így $AT=\frac{1}{2}$ és $BT=\frac{\sqrt[]{3}}{2}$. A BC egyenes felezi az $ABT$ szöget, mert $CBT\sphericalangle =ABT\sphericalangle -ABC\sphericalangle ={30}^{\circ }-{15}^{\circ }={15}^{\circ }=ABC\sphericalangle$. A szögfelezőtételt alkalmazva kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{TC}{CA}=\frac{BT}{BA}\mathrm{,}\text{azaz}\frac{y}{x}=\frac{\sqrt[]{3}}{2}\mathrm{.}}\end{array}$ (1) Tudjuk, hogy $AT=AC+CT=\frac{1}{2}$, vagyis $\begin{array}{c}{\displaystyle x+y=\frac{1}{2}\mathrm{.}}\end{array}$ (2) Az (1) és (2) egyenletekből álló egyenletrendszert megoldva $\begin{array}{c}{\displaystyle x=2-\sqrt[]{3}\text{<span style="font-weight: normal;font-style: normal;">és</span>}y=\frac{2\sqrt[]{3}-3}{2}}\end{array}$ adódik. A $BC$ oldal hosszát ezután a $BCT$ háromszögből, Pitagorasz tételét alkalmazva kapjuk: $\begin{array}{c}{\displaystyle B{C}^2=C{T}^2+T{B}^2={\left(\frac{2\sqrt[]{3}-3}{2}\right)}^2+{\left(\frac{\sqrt[]{3}}{2}\right)}^2=6-3\sqrt[]{3}\mathrm{.}}\end{array}$ Tehát az $ABC$ háromszög másik két oldalának hossza $2-\sqrt[]{3}$ és $\sqrt[]{6-3\sqrt[]{3}}$.  Szilasi Zoltán (Debrecen, KLTE Gyak. Gimn., 9. évf.)