Kezdőlap


Feladat:	Gy.3146	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Papp Dávid
Füzet:	1998/március, 149. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Beírt kör, Terület, felszín, Háromszög-egyenlőtlenség alkalmazásai, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/szeptember: Gy.3146

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög átfogóját $c$ -vel, területét pedig $t$ -vel. Ismert, hogy minden háromszögben igaz a $2 t = r \cdot (a + b + c)$ összefüggés (a bizonyítás leolvasható az ábráról), ezért mivel a háromszögünk derékszögű

\begin{matrix} r = \frac{a \cdot b}{a + b + c}, azaz \frac{2 a b}{(a + b) \cdot r} = \frac{2 (a + b + c)}{a + b} . \end{matrix}

Így a bizonyítandó összefüggés a

\begin{matrix} 2 + \sqrt[]{2} \leq \frac{2 (a + b + c)}{a + b} < 4, \end{matrix}

azaz a

\begin{matrix} \sqrt[]{2} \leq \frac{2 c}{a + b} < 2 \end{matrix}

alakot ölti. A jobb oldali egyenlőtlenség nyilvánvalóan következik a

c < a + b

háromszög-egyenlőtlenségből. A bal oldali egyenlőtlenség ekvivalens a

2 {(a + b)}^{2} \leq 4 c^{2}

egyenlőtlenséggel, amit Pitagorasz tételét felhasználva

{(a + b)}^{2} \leq 2 (a^{2} + b^{2})

alakban is írhatunk. Ezt rendezve a mindig teljesülő

0 \leq {(a - b)}^{2}

egyenlőtlenséget kapjuk.
Minden lépésben ekvivalens átalakításokat végeztünk, ezért a feladatban szereplő mindkét egyenlőtlenséget igazoltuk.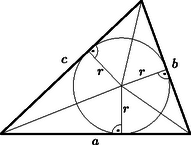