Kezdőlap


Feladat:	Gy.3132	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Tóth Viktória
Füzet:	1998/február, 91 - 92. oldal		PDF \| MathML
Témakör(ök):	Paralelogrammák, Húrnégyszögek, Háromszögek hasonlósága, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/április: Gy.3132

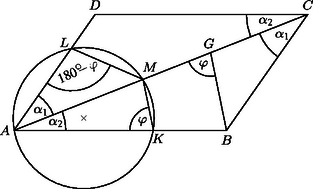
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A K M ∢ = φ$ . Mivel $A K M L$ húrnégyszög, azért $A L M ∢ = 180^{\circ} - φ$ , továbbá $L A M ∢ = L K M ∢ < φ$ és $K A M ∢ = K L M ∢ < 180^{\circ} - φ$ . A paralelogramma szemközti oldalai párhuzamosak, ezért $D A C ∢ = A C B ∢$ és $C A B ∢ = A C D ∢$ . Ebből és az előző egyenlőtlenségekből következik, hogy az $A C$ átlónak van egy olyan $G$ belső pontja, amire $A G B ∢ = φ$ és $B G C ∢ = 180^{\circ} - φ$ . Ekkor viszont az $A K M$ és az $A G B$ , továbbá az $A L M$ és a $C G B$ háromszögpárok hasonlóak, mert megfelelő szögeik egyenlőek. Hasonló háromszögekben a megfelelő oldalak aránya egyenlő, ezért

\begin{matrix} \frac{A K}{A M} = \frac{A G}{A B} és \frac{A L}{A M} = \frac{C G}{C B} . \end{matrix}

E két egyenlőségből kapjuk, hogy

\begin{matrix} A B \cdot A K = A G \cdot A M és C B \cdot A L = C G \cdot A M . \end{matrix}

Ezeket összeadva és felhasználva, hogy

C B = A D

\begin{matrix} A B \cdot A K + A D \cdot A L = A G \cdot A M + C G \cdot A M = A C \cdot A M, \end{matrix}

ami éppen a bizonyítandó állítás.

Tóth Viktória (Zalaegerszeg, Zrínyi M. Gimn., I. o.t.) dolgozata alapján