Kezdőlap


Feladat:	F.3171	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Gyenes Zoltán , Juhász András
Füzet:	1998/március, 153 - 156. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Négyzetek, Derékszögű háromszögek geometriája, Beírt alakzatok, Geometriai egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1997/március: F.3171

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat megoldásához néhány segédtételt bocsátunk előre.
I. Egy téglalapban elhelyezett bármely négyzet oldala legfeljebb akkora, mint a téglalap rövidebbik oldala.
Húzzunk párhuzamost a négyzet csúcsain keresztül a téglalap megfelelő oldalaival úgy, hogy azok ne messék a négyzet belsejét. A négy egyenes olyan négyzetet határoz meg, amely a kiindulási négyzetet tartalmazza, és oldalai párhuzamosak a téglalap oldalaival.
II. Egy derékszögű háromszögbe írt négyzetek közül az a legnagyobb, amelyiknek két oldala a befogókra illeszkedik, egy csúcsa pedig az átfogón van.
Legyen $K L M N$ egy, az $A B C$ derékszögű háromszögben lévő négyzet. Mozgassuk el a négyzetet úgy, hogy pl. $K$ az $A C$ , $L$ pedig a $B C$ oldalon legyen, és az új négyzet is $A B C$ -ben feküdjön (1. ábra). Mivel $C K O L$ húrnégyszög, $O C K ∢ = O L K ∢ = 45^{\circ}$ , vagyis a négyzet $O$ középpontja a derékszög felezőjére esik. Messe ez a szögfelező az $M N$ oldalt $D$ -ben. Elegendő megmutatni, hogy $\bar{C D} > \bar{K M}$ . Látható, hogy $C$ , $K$ , $D$ és $M$ egy körön van, hiszen a $K D$ szakasz $C$ -ből is és $M$ -ből is $45^{\circ}$ -os szögben látszik. A $C$ , $K$ , $D$ és $M$ pontokon átmenő kör $O'$ középpontja a $C D$ és $K M$ húrok felezőmerőlegesének metszéspontja, ezért $O' F O ∢ = 90^{\circ}$ , így $\bar{O' F} < \bar{O' O}$ . A $C D$ húr tehát közelebb van $O'$ -höz, mint a $K M$ , ezért valóban $\bar{C D} > \bar{K M}$ .
III. Ha egy egységnyi oldalú négyzetben elhelyezkedik egy $a$ és egy $b$ oldalú, közös belső pont nélküli négyzet, akkor $a + b \leq 1$ .
Legyen $e$ olyan egyenes, amelynek a két négyzet különböző félsíkjában van (2. ábra). Ha $e$ az egységnégyzet valamelyik oldalával párhuzamos, akkor (I) szerint készen vagyunk. Egyébként $e$ metszi az egységnégyzet valamennyi oldalegyenesét. Jelölje $C_{1}$ és $C_{2}$ az egységnégyzet két azon átellenes csúcsát, amelyek egyike az $e$ -től legtávolabb lévő csúcs. (II) szerint a $C_{1} E F$ , illetve a $C_{2} G H$ derékszögű háromszögben elhelyezhető legnagyobb négyzet egyik átlója a $C_{1} C_{2}$ szakaszon van, így a két átlónak közös belső pontja nem lévén, hosszuk összege legfeljebb $\bar{C_{1} C_{2}}$ , azaz $\sqrt[]{2} (a + b) \leq \sqrt[]{2}$ .
IV. Egy téglalapban lévő, közös belső pont nélküli két négyzet oldalának összege legfeljebb akkora, mint a téglalap hosszabbik oldala.
Az állítás közvetlenül adódik (III)-ból, ehhez a téglalapot olyan négyzetté egészítjük ki, amelynek oldala a téglalap hosszabbik oldalával egyenlő.

Nevezzük a továbbiakban az

1 \times 2

-es téglalap felezőjének azt az egyenest, amely őt 2 darab egységnégyzetre bontja; e két négyzetet hívjuk majd a téglalap felének.
V. Ha az

1 \times 2

-es téglalapban lévő valamely négyzetnek létezik közös (határ)pontja a téglalap egységnyi hosszúságú oldalával, akkor ez a négyzet a téglalapnak az egyik (a közös pontot tartalmazó) felében van.
Az (I) bizonyításában látott módon a szóban forgó négyzet olyan, a téglalapban fekvő négyzetbe foglalható, amelynek oldalai párhuzamosak a téglalap oldalaival, és egyik oldalegyenese a téglalap egyik egységhosszúságú oldalával közös. Nyilván ez a befoglaló négyzet a téglalap felében található.
A feladat kérdésére térve megmutatjuk, hogy a válasz igenlő. Toljuk el a téglalapban lévő három négyzetből álló ponthalmazt a

\vec{B A}

irányában úgy, hogy valamelyik négyzetnek legyen határpontja

A D

-n (3. ábra). Ha több ilyen négyzet is lenne, jelöljük ki az egyiket; nevezzük bal szélsőnek. A másik két négyzet közül válasszuk ki azt, amelyiket

\vec{A B}

irányában eltolva nem metszi a másikat (ha mindkettő ilyen, tekintsük az egyiket); toljuk el ezt a négyzetet úgy, hogy egyik határpontja

B C

-re essék. Az így kapott négyzetet hívjuk jobb szélsőnek, az első eltolás során kapott harmadikat pedig középsőnek. A négyzetek származtatásából látható, hogy a bal szélsőnek és a középsőnek nincs közös belső pontja, akárcsak a jobb szélsőnek és a középsőnek. A két szélső pedig azért nem metszi egymást, mert (V) szerint a téglalap két különböző felében vannak. A továbbiakban elegendő csak a két szélső és a középső négyzettel foglalkozni az eredetiek helyett; mivel nem metszik egymást, a középső elválasztható a két szélsőtől az

e

és az

f

egyenesekkel. Mivel a két szélső négyzet a téglalap ,,bal'', illetve ,,jobb' felében fekszik, elérhető, hogy

e

-nek legyen közös pontja a téglalap bal felét alkotó zárt négyzetlemezzel, hasonlóan

f

-nek a zárt jobb féllel.
Ha

e

és

f

egyike párhuzamos

A D

-vel, akkor a bizonyítani kívánt egyenlőtlenség következik (IV)-ből; ha pedig az egyik egyenes

A B

-vel párhuzamos, akkor egy négyzet egy

n \times 2

-es, kettő pedig egy

(1 - n) \times 2

-es téglalapba kerül, ezért (I) szerint a négyzetoldalak összege legfeljebb

n + 2 (1 - n) = 2 - n \leq 2

. Foglalkozzunk a továbbiakban azzal az esettel, amikor

e

és

f

a téglalap valamennyi oldalegyenesét metszve létrehoz két olyan derékszögű háromszöget, amelyekben egy-egy szélső négyzet helyezkedik el. Tekintsük például a 3. ábrán az

A

csúcsú,

e

által levágott derékszögű háromszöget. Mivel

e

-nek van közös pontja a téglalap bal felével, azért a

D A B

szög felezője a téglalapon metszi az

e

egyenest. Ez azt jelenti, hogy a derékszögű háromszögbe a (II) szerinti legnagyobb négyzetet beírva, az része marad a téglalapnak; helyettesítsük ővele a bal szélső négyzetet, és tegyünk ugyanígy a jobb szélső négyzettel is. Ezután két esetet különböztetünk meg aszerint, hogy az újonnan kapott szélső négyzetek a téglalap különböző vagy azonos oldalaira támaszkodnak-e (4. és 5. ábra). Az első esetben a középső négyzet

c

oldala legfeljebb akkora, mint az

X Z Y

derékszögű háromszög

X Z

befogója (4. ábra). Az

X T Y

derékszögű háromszög

X Y

átfogója az

X Z Y

háromszögével közös, így ‐ mivel

Z X Y ∢ \geq T X Y ∢

‐

\bar{Z Y} \geq \bar{T Y}

, ezért

\begin{matrix} c \leq c' = \bar{X Z} \leq \bar{X T} = 2 - (a + b) . \end{matrix}

Utolsóként az 5. ábrán látható konfigurációval foglalkozunk. Megmutatjuk, hogy az

a

és

b

oldalú négyzetekhez nem tudunk

2 - a - b

vagy annál nagyobb oldalú négyzetet illeszteni úgy, hogy az ne nyúljon ki a téglalapból. A 6. ábra jelöléseivel elég azt megmutatni, hogy már a

c' = 2 - (a + b)

oldalú négyzet is csak úgy helyezhető el ezen a módon, hogy

H

csúcsának

A B

-től való távolsága nagyobb, mint 1; feltehető, hogy

a

b < 1

.
Könnyen látható, hogy a

c'

oldalú négyzetbe berajzolt négy, egymással egybevágó derékszögű háromszög hasonló a

P Q S

és a

T R P

derékszögű háromszögekhez; ezekben a két befogó arányát jelölje

t

, és használjuk az ábra többi jelölését is. A

H

pontnak az

A B

-től való távolsága:

\begin{matrix} \begin{matrix} d = c' \cdot \frac{t + 1}{\sqrt[]{1 + t^{2}}} + (a - \frac{y}{t}) = \\ = c' \frac{t + 1}{\sqrt[]{1 + t^{2}}} + (b - t x) . \end{matrix} \end{matrix}

Figyelembe véve, hogy

a - \frac{y}{t} = b - t x

P

pont távolsága

A B

-től) és

\begin{matrix} x + y = c' = 2 - (a + b), \end{matrix}

kapjuk, hogy

\begin{matrix} x = \frac{t (b - a) + c'}{1 + t^{2}}, \end{matrix}

ezért

\begin{matrix} \begin{matrix} d - 1 = (\frac{t^{2} + t}{1 + t^{2}} - \frac{1 + t}{\sqrt[]{1 + t^{2}}}) a + (\frac{1 + t}{1 + t^{2}} - \frac{1 + t}{\sqrt[]{1 + t^{2}}}) b + 2 (\frac{1 + t}{\sqrt[]{1 + t^{2}}} - \frac{t}{1 + t^{2}}) - 1 = \\ = (t + 1) [(\frac{t}{1 + t^{2}} - \frac{1}{\sqrt[]{1 + t^{2}}}) a + (\frac{1}{1 + t^{2}} - \frac{1}{\sqrt[]{1 + t^{2}}}) b + 2 (\frac{1}{\sqrt[]{1 + t^{2}}} - \frac{1}{1 + t^{2}}) - \frac{t - 1}{1 + t^{2}}] = \\ = (t + 1) [(\frac{1}{\sqrt[]{1 + t^{2}}} - \frac{1}{1 + t^{2}}) (2 - a - b) - \frac{t - 1}{1 + t^{2}} (1 - a)] = \\ = \frac{t + 1}{1 + t^{2}} [(\sqrt[]{1 + t^{2}} - 1) (2 - a - b) - (t - 1) (1 - a)] > 0, \end{matrix} \end{matrix}

hiszen

\sqrt[]{1 + t^{2}} - 1 > 0

\sqrt[]{1 + t^{2}} - 1 > t - 1

és

2 - a - b > 1 - a

Gyenes Zoltán (Budapest, Apáczai Cs. J. Gyak. Gimn., III. o.t.) és

Juhász András (Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozatainak felhasználásával

Megjegyzések. 1. A feladat rokonságot mutat az 1974. évi Kürschák József matematika verseny 2. feladatával, amely megtalálható Surányi János: Matematikai versenytételek III. rész c. művében.
2. Ha a téglalap

1 \times d

méretű és

d < 2

, akkor

a + b + c \leq d

nem igaz.
3. Megyeri Csaba (Nagykanizsa, Batthyány L. Gimn., IV. o.t.) rámutat a feladat és Erdős Pál megoldatlan feladata közötti kapcsolatra: Ha a feladat állítása nem lenne igaz, akkor Erdős professzor úr megoldatlan problémája sem lenne igaz. Osszuk fel ugyanis az egységnégyzetet

n^{2}

darab

\frac{1}{n}

oldalú négyzetre. Két egymás mellettibe elhelyezzük azt a három négyzetet, amelyre

a + b + c > \frac{2}{n}

, a többi négyzetet meghagyjuk. Így összesen

n^{2} + 1

négyzetet helyeztünk el, az oldalhosszak összege: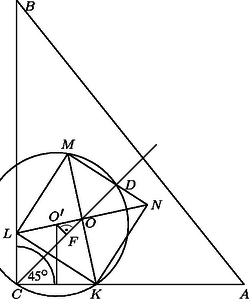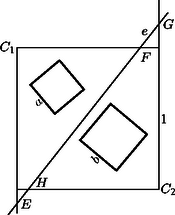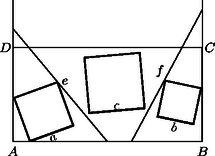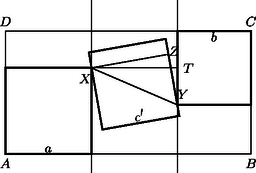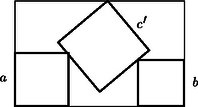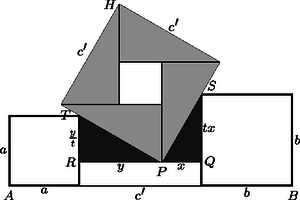

\begin{matrix} a_{1} + a_{2} + ... + a_{n^{2} + 1} = a + b + c + (n^{2} - 2) \cdot \frac{1}{n} > \frac{2}{n} + (n^{2} - 2) \cdot \frac{1}{n} = n . \end{matrix}