Kezdőlap


Feladat:	Gy.3122	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1998/február, 90 - 91. oldal		PDF \| MathML
Témakör(ök):	Húrsokszögek, Középponti és kerületi szögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/március: Gy.3122

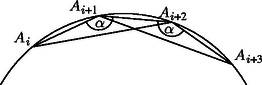
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy az állítás igaz. Jelöljük a sokszög csúcsait $A_{1}$ , $A_{2}$ , $...$ , $A_{1997}$ -tel, a csúcsoknál lévő szöget pedig $α$ -val. Az $A_{i} A_{i + 2}$ húr az $A_{i + 1}$ csúcsból $α$ szögben látszik ( $i = 1$ , 2, $...$ , 1997, az indexeket modulo 1997 számolva), $A_{i + 1}$ mindig a rövidebbik $A_{i} A_{i + 2}$ íven van, mert $α$ tompaszög, ezért az $A_{i} A_{i + 2}$ húrok mind egyenlő hosszúságúak, és a rövidebb $A_{i} A_{i + 2}$ körívek is mind egyenlő hosszúságúak. A továbbiakban $P Q$ -val jelöljük a kör $P$ és $Q$ pontjai által meghatározott rövidebb körív hosszát.
Mivel $A_{1} A_{3} = A_{2} A_{4}$ , azért a hosszabbik $A_{1} A_{3}$ és $A_{2} A_{4}$ ívek is egyenlő hosszúságúak, vagyis

\begin{matrix} \begin{matrix} A_{3} A_{4} + A_{4} A_{5} + ... + A_{1996} A_{1997} + A_{1997} A_{1} = \\ = A_{4} A_{5} + ... + A_{1997} A_{1} + A_{1} A_{2}, \end{matrix} \end{matrix}

amiből kapjuk, hogy

A_{3} A_{4} = A_{1} A_{2}

. Az ennek megfelelő egyenlőséget a hosszabbik

A_{i} A_{i + 2}

és

A_{i + 1} A_{i + 3}

ívekre felírva kapjuk, hogy

\begin{matrix} A_{i + 2} A_{i + 3} = A_{i} A_{i + 1} \end{matrix}

minden

i

-re, vagyis minden második rövid ív hossza megegyezik. De mivel páratlan sok rövid ívünk van, ez egyúttal azt is jelenti, hogy minden rövid ív hossza megegyezik. Ebből viszont következik, hogy a körbe írható sokszögünk minden oldala egyenlő hosszúságú, tehát a sokszög szabályos.

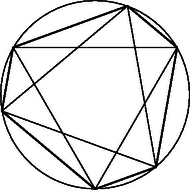
Megjegyzés. A bizonyításunk minden körbe írható páratlan oldalú sokszög esetén alkalmazható. Páros oldalú sokszög esetén viszont feltételeinkből nem következik a szabályosság. A legegyszerűbb ellenpélda egy téglalap, de ellenpélda a 2. ábrán látható hatszög is, általában pedig egy olyan

2 n

-szög, amit úgy kapunk, hogy egy szabályos

n

-szöget a középpontja körül

\frac{180^{\circ}}{n}

-nél kisebb szöggel elforgatunk, majd pedig tekintjük az eredeti sokszög és az elforgatottja csúcsai által meghatározott konvex sokszöget.