Feladat:	3281. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Belkovits Katalin ,  Patay Gergely
Füzet:	2000/május, 311 - 313. oldal		PDF  |  MathML
Témakör(ök):	Gördülés (Merev testek síkmozgása), Feladat
Hivatkozás(ok):	Feladatok: 1999/október: 3281. fizika feladat

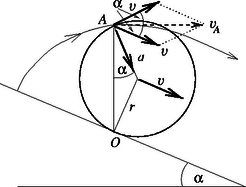
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás A karika adott pontjának pályagörbéjét nyilván nem befolyásolja az, hogy a karika gyorsul-e vagy nem. Az egyszerűség kedvéért tételezzük fel, hogy a karika egyenletes $v$ sebességgel gördül le a lejtőn. Az $A$ pont a pálya legmagasabb pontja, ezért itt kérdéses (éppen itt levő) tömegpontnak nem lehet függőlegesen felfele mutató sebesség-komponense. (Ha nem így lenne, akkor egy kicsivel később még magasabbra kerülne). Hasonló okokból lefelé mutató sem lehet a függőleges sebesség-összetevője. A karika kérdéses darabkájának sebesség tehát vízszintes kell legyen az $A$ pontban. A karika bármely pontjának sebessége a karika középpontjának $v$ nagyságú, a vízszinteshez képest $\alpha$ szögben lefelé irányuló sebességéből, valamint a középpont körüli forgómozgás ugyancsak $v$ nagyságú kerületi sebességéből tevődik össze. A két sebesség vektori összege akkor lesz vízszintes, ha a kerületi sebesség vektora a vízszintessel ugyancsak $\alpha$ szöget zár be (emelkedő irányban). Az eredő sebesség nagysága ezek szerint $\begin{array}{c}{\displaystyle v_A=2v\text{cos}\alpha \mathrm{.}}\end{array}$ A vizsgált pont gyorsulása a karikával együtt mozgó vonatkoztatási rendszerből nézve forgómozgás centripetális gyorsulása, tehát $\begin{array}{c}{\displaystyle a=\frac{v^2}{r}\mathrm{.}}\end{array}$ Ez a gyorsulásvektor a karika középpontja felé mutat, tehát a függőlegessel $\alpha$ szöget zár be. A gyorsulás a lejtőhöz rögzített (álló) koordináta-rendszerből nézve ugyanakkora, mint az egyenletesen mozgó rendszerben. Az álló rendszerben a vizsgált pont gyorsulása két összetevőre bontható. A sebességre merőleges (tehát függőleges) komponens a pálya $R$ görbületi sugarával így fejezhető ki: $\begin{array}{c}{\displaystyle a_f=\frac{v_A^2}{R}\mathrm{.}}\end{array}$ Másrészt viszont ugyanez a mennyiség a gyorsulás nagyságának és irányának ismeretében $\begin{array}{c}{\displaystyle a_f=a\text{cos}\alpha =\frac{v^2}{r}\text{cos}\alpha }\end{array}$ módon is megadható. A kétféle kifejezés összevetéséből ($v_A$ korábban kiszámított értékének felhasználásával) a pálya görbületi sugarára $\begin{array}{c}{\displaystyle R=4r\text{cos}\alpha }\end{array}$ adódik.  Patay Gergely (Debrecen, Tóth Á. Gimn., 12. o.t.)   Megjegyzés. A karika vizsgált pontja ciklois alakú görbén mozog. A karikának a lejtővel éppen érintkező $O$ pontja nem mozog (sebessége nulla), tehát ezen a ponton halad át a karika pillanatnyi forgástengelye. Ennek ellenére nem mondhatjuk, hogy a pályagörbe görbületi sugara az $A$ pontban az $AO$ szakasz hosszával (tehát $2r\text{cos}\alpha$-val) egyenlő, hanem ‐ mint az a fenti megoldásból kiderült ‐ annak éppen a kétszerese. A meglepőnek tűnő eltérés onnan származik, hogy a karika és a lejtő érintkezési pontja nem rögzített pont, hanem a karika elfordulása közben maga is elmozdul. 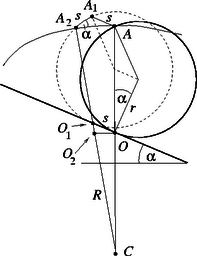Jól szemlélteti a pillanatnyi forgástengelyre hivatkozó (hibás) érvelés tarthatatlanságát a következő példa: Egy kerékpár valamelyik kerekének tengelye is mindig a keréknek a talajjal érintkező pontja körül fordul el, mégsem állíthatjuk, hogy a tengely által leírt pályagörbe (ami egyenes) a kerék sugarával egyenlő görbületi sugárral rendelkezne!   II. megoldás. A cikloisnak, mint egy egyenesen gördülő kör egy pontja által leírt görbének az $A$ pontbeli érintője vízszintes. A karika ebben a helyzetben az $O$ pont körül fordul el, az $AO$ szakasz tehát függőleges kell legyen. Rajzoljuk fel a karika kicsit korábbi helyzetét is, amikor a lejtővel még az $O_1$ pontban érintkezett, és jelöljük az $O{O}_1$ távolságot $s$-sel ($s\ll r)$. Ha a karikát elfordulás nélkül eltolnánk a lejtőn felfelé $s$ távolsággal, akkor az $A$ pont $A_1$-be kerülne ($A{A}_1=s$). Ebben a korábbi helyzetben a cikloist leíró pont (a tiszta gördülés feltétele miatt) nem $A_1$-ben, hanem attól (a kör mentén ívesen mérve) $s$ távolságban levő az $A_2$ pontban helyezkedik el. A kicsiny íveket egyenes szakaszokkal közelítve megállapíthatjuk, hogy az $A{A}_1{A}_2▵$ egyenlőszárú, melynek $s$ hosszú szárai $\alpha$ szöget zárnak be a vízszintes $A{A}_2$ oldallal. A cikloist leíró pont $A_2$-beli sebessége merőleges az $A_2{O}_1$ egyenesre (hiszen $O_1$ pillanatnyi sebessége nulla), az $A$-beli sebesség pedig $AO$-ra merőleges. Ha a ciklois az $A$ pont kis környezetében jól közelíthető egy alkalmasan választott körrel (a simulókörrel), akkor annak $C$ középpontja nem lehet máshol, mint az $AO$ egyenes és az $A_2{O}_1$ egyenes metszéspontjában. Húzzunk az $O$ pontból egy vízszintes egyenest, és jelöljük ezen egyenes és az $A_2{O}_1$ egyenes metszéspontját $O_2$-vel. A $CO{O}_2$ és a $CA{A}_2$ háromszögek hasonlóságából $\begin{array}{c}{\displaystyle \frac{OC}{AC}=\frac{O{O}_2}{A{A}_2}}\end{array}$ következik, ami $O{O}_2\approx s\text{cos}\alpha$, $A{A}_2\approx 2s\text{cos}\alpha$ és $AO=2r\text{cos}\alpha$ felhasználásával meghatározza a keresett $R=AC$ görbületi sugarat: $\begin{array}{c}{\displaystyle \frac{R-2r\text{cos}\alpha }{R}=\frac{s\text{cos}\alpha }{2s\text{cos}\alpha }=\frac{1}{2}\mathrm{,}\text{azaz}R=4r\text{cos}\alpha \mathrm{.}}\end{array}$  Belkovits Katalin (Marosvásárhely, Bolyai Farkas Elm. Líceum, 11. o.t.)     dolgozata alapján