Kezdőlap


Feladat:	3232. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gergely , Buruzs Ádám , Gáspár Merse Előd , Hegedűs Ákos , Katona Gergely , Máthé András , Tóth Bálint
Füzet:	2000/május, 305 - 307. oldal		PDF \| MathML
Témakör(ök):	Gördülés lejtőn, Egyéb súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1999/február: 3232. fizika feladat

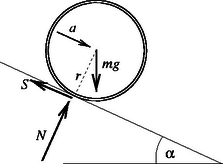
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az abroncsra az 1. ábrán látható erők hatnak. Mivel a lejtőre merőleges irányban nem gyorsul a test,

\begin{matrix} N = m g cos α, \end{matrix}

(1)

a súrlódási erő pedig (mindaddig, amíg csúszik az abroncs)

\begin{matrix} S = μ N = μ m g cos α . \end{matrix}

(2)

A lejtő irányú mozgásegyenletből következik, hogy az abroncs tömegközéppontjának gyorsulása

\begin{matrix} a = g (sin α - μ g cos α) . \end{matrix}

(3)

A súrlódási együttható megadott helyfüggését is figyelembe véve és bevezetve az

\begin{matrix} ω_{0} = \sqrt[]{γ g cos α} és x_{0} = \frac{tg α}{γ} \end{matrix}

(4)

jelöléseket a (3) mozgásegyenlet

\begin{matrix} a = - ω_{0}^{2} (x - x_{0}) \end{matrix}

(5)

alakba is írható. Ez az egyenlet megegyezik egy

ω_{0}

körfrekvenciájú,

x_{0}

egyensúlyi helyzetű harmonikus rezgőmozgáséval. Ezt az analógiát kihasználva felírhatjuk az abroncs tömegközéppontjának

x (t)

elmozdulását is. Az

x (0) = 0

és

v (0) = 0

kezdeti feltételeket figyelembe véve a megoldás:

\begin{matrix} x (t) = x_{0} (1 - cos ω_{0} t), \end{matrix}

(6)

az abroncs tömegközéppontjának pillanatnyi sebessége pedig

\begin{matrix} v (t) = x_{0} ω_{0} sin ω_{0} t . \end{matrix}

(7)

A elmozdulás ismeretében kiszámíthatjuk a pillanatról pillanatra változó súrlódási együtthatót, abból a súrlódási erőt:

\begin{matrix} \begin{matrix} (8) S (t) = μ m g cos α = x (t) \cdot γ m g cos α, \\ majd ennek forgatónyomatékából az abroncsβszöggyorsulását: \\ (9) β = \frac{r S}{m r^{2}} = \frac{γ x_{0} g cos α}{r} (1 - cos ω_{0} t) . \end{matrix} \end{matrix}

(Kihasználtuk, hogy egy

m

tömegű,

r

sugarú vékony abroncs tehetetlenségi nyomatéka

m r^{2}

.)
A (9) képlet azt mutatja, hogy a szöggyorsulás egy időben állandó és egy időben periodikusan (

cos ω_{0} t

-vel arányosan) változó tag összege. Ennek megfelelően az abroncs szögsebessége (annak kezdeti nulla értékét is figyelembe véve)^{$^{*}$} Az abroncs pillanatról pillanatra változó

ω (t)

szögsebessége nem tévesztendő össze a tömegközéppont mozgásképletében szerepló

ω_{0}

körfrekvenciával, ami egy állandó érték.:

\begin{matrix} ω (t) = \frac{γ x_{0} g}{r} cos α (t - \frac{sin ω_{0} t}{ω_{0}}) . \end{matrix}

(10)

Az abroncs addig csúszik, míg a tömegközéppont

v (t)

sebessége nagyobb, mint a forgómozgásból származó

v_{ker} (t) = r ω (t)

kerületi sebesség. A tiszta gördülés kezdetére (7) és (10) szerint

\begin{matrix} x_{0} ω_{0} sin ω_{0} t = γ x_{0} g cos α (t - \frac{sin ω_{0} t}{ω_{0}}) \end{matrix}

(11)

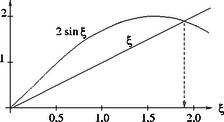
jellemző, amit (4) felhasználásával és a az

ξ = ω_{0} t

új változó bevezetésével

\begin{matrix} ξ = 2 sin ξ \end{matrix}

(12)

alakra hozhatunk. (12) megoldása grafikusan (2. ábra), vagy egy zsebszámológéppel numerikusan kereshető meg, és

ξ \approx 1, 8955

-nek adódik.
Az abroncs tehát az indításától számított

\begin{matrix} t \approx \frac{1, 90}{ω_{0}} = \frac{1, 90}{\sqrt[]{γ g cos α}} \end{matrix}

(13)

idő múlva kezd el csúszásmentesen gördülni.
A mozgás további részében (egészen a lejtő aljáig) az abroncs sebessége és a szögsebessége (

\frac{1}{2} g sin α

gyorsulással, illetve

\frac{g}{2 r} sin α

szöggyorsulással) időben egyenletesen növekszik.

Ambrus Gergely (Szeged, Radnóti M. Gimn., 10. o.t.) és

Katona Gergely (Budapest, ELTE Trefort Á. Gyakorlóisk., 12. o.t.) dolgozata alapján

^{$^{*}$}

^{*}