Feladat:	3293. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hegedűs Ákos ,  Nagy Ádám ,  Pozsgay Balázs ,  Reischig Péter
Füzet:	2000/március, 186 - 188. oldal		PDF  |  MathML
Témakör(ök):	Egyéb merev test síkmozgások, Tömegközéppont mozgása, Feladat
Hivatkozás(ok):	Feladatok: 1999/november: 3293. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A rendszerre nem hatnak vízszintes irányban külső erők, emiatt a tömegközéppont kezdeti $v_0/2$ vízszintes sebessége időben változatlan marad. Üljünk bele a tömegközépponttal együtt vízszintes irányban egyenletesen mozgó koordináta-rendszerbe. Jelöljük a kis test vízszintes elmozdulását $x$-szel, ekkor az abroncs középpontja ellenkező irányban ugyanennyivel kell elmozduljon, hiszen az egész rendszer tömegközéppontja vízszintes irányban mozdulatlan. 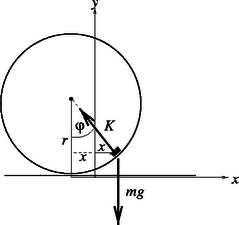A kis testre az (1. ábrán) látható erők hatnak. Ha $v_0$ kicsi, akkor a kis test csak kicsit mozdulhat ki vízszintes irányban, a függőleges elmozdulása (és ezzel együtt a függőleges irányú gyorsulása) tehát másodrendűen kicsiny, elhanyagolható. Emiatt a $K$ kényszererő az $mg$ nehézségi erővel egyezik meg, vízszintes komponense pedig $\begin{array}{c}{\displaystyle K_x=-K\text{sin}\phi \approx mg\frac{2x}{r}\mathrm{.}}\end{array}$ Newton második törvénye szerint $\begin{array}{c}{\displaystyle ma=-\frac{2mg}{r}x\mathrm{,}}\end{array}$ amelyben felismerhetjük az $\omega =\sqrt[]{2g/r}$ körfrekvenciájú harmonikus rezgések mozgásegyenletét. A kis test kezdeti sebessége (a tömegközépponti rendszerben) $v_0/2$, a kitérés időbeli alakulását tehát az $\begin{array}{c}{\displaystyle x\left(t\right)=\frac{v_0}{2\omega }\text{sin}\omega t}\end{array}$ függvény írja le. 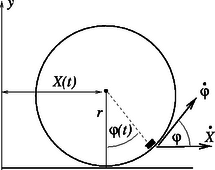Visszatérve az eredeti (az asztallaphoz rögzített) koordináta-rendszerbe, az abroncs középpontjának elmozdulása $\begin{array}{c}{\displaystyle X\left(t\right)=\frac{v_{0}t}{2}-\frac{v_0}{2\omega }\text{sin}\omega t\mathrm{,}}\end{array}$ a sebessége pedig $\begin{array}{c}{\displaystyle V\left(t\right)=\frac{v_0}{2}\left(1-\text{cos}\omega t\right)\mathrm{.}}\end{array}$   II. megoldás. Jelöljük az abroncs tömegközéppontjának $t$ pillanatbeli elmozdulását $X\left(t\right)$-vel, pillanatnyi sebességét pedig $V\left(t\right)$-vel; a kis test és az abroncs középpontját összekötő egyenes függőlegessel bezárt szögét pedig $\phi$-vel (2. ábra). Ez a két (pillanatról pillanatra változó) adat leírja a rendszer mozgását, feladatunk tehát ezen függvények meghatározása. Jelöljük az egyes mennyiségek idő szerinti változási sebességét (egységnyi idő alatti változást) a kérdéses mennyiség betűjele fölé írt ,,ponttal''. Ezzel a jelöléssel az abroncs pillanatnyi (vízszintes) sebessége $\dot{X}\left(t\right)$, a kis testnek a karikához viszonyított szögsebessége $\dot{\phi }$, érintő irányú kerületi sebessége tehát $r\dot{\phi }$. Az abroncsra (súrlódásmentes körülmények között) nem hat forgatónyomaték, ezért nem jön forgásba. A rendszerre vízszintes irányban nem hat külső erő, emiatt a teljes vízszintes irányú impulzus időben állandó marad. $\begin{array}{c}{\displaystyle m\dot{X}+m\left(\dot{X}+r\dot{\phi }\text{cos}\phi \right)=I=\text{állandó}\mathrm{.}}\end{array}$ (1) Ugyancsak változatlan marad a rendszer teljes mechanikai energiája: $\begin{array}{c}{\displaystyle \frac{1}{2}m{\dot{X}}^2+\frac{1}{2}m\left({\dot{X}}^2+r^2{\dot{\phi }}^2+2\dot{X}r\dot{\phi }\text{cos}\phi \right)+mgr\left(1-\text{cos}\phi \right)=E=\text{állandó}\mathrm{.}}\end{array}$ (2) Kezdetben $\dot{X}\left(t=0\right)=0$ és $\dot{\phi }\left(t=0\right)=v_0/r$, innen a két mozgásállandó: $I=m{v}_0$, illetve $E=\frac{1}{2}m{v}_0^2$. Ezek felhasználásával írhatjuk $\begin{array}{c}{\displaystyle 2\dot{X}+r\dot{\phi }\text{cos}\phi =v_0\mathrm{,}}\end{array}$ (3) valamint $\begin{array}{c}{\displaystyle 2{\dot{X}}^2+r^2{\dot{\phi }}^2+2\dot{X}rbf\dot{\phi }\text{cos}\phi +2rg\left(1-\text{cos}\phi \right)=v_0^2\mathrm{.}}\end{array}$ (4) Fejezzük ki (3)-ból $\dot{X}\left(t\right)$-t és helyettesítsük (4)-be: $\begin{array}{c}{\displaystyle \dot{X}=\frac{v_0-r\dot{\phi }\text{cos}\phi }{2}\mathrm{,}}\end{array}$ (5) $\begin{array}{c}{\displaystyle r^2{\dot{\phi }}^2\left(2-\text{cos}\phi \right)+4rg\left(1-\text{cos}\phi \right)=v_0^2\mathrm{.}}\end{array}$ (6) Használjuk ki továbbá, hogy $v_0$ kicsiny ($v_0\ll \sqrt[]{gr}$), így $1-\text{cos}\phi \ll 1$, tehát $\begin{array}{c}{\displaystyle 1-\text{cos}\phi =2\text{sin}{}^2\frac{\phi }{2}\approx \frac{{\phi }^2}{2}\mathrm{.}}\end{array}$ Ebben a közelítésben (6) így alakul: $\begin{array}{c}{\displaystyle {\dot{\phi }}^2+\frac{2g}{r}{\phi }^2={\left(\frac{v_0}{r}\right)}^2\mathrm{.}}\end{array}$ (7) Ez az összefüggés megegyezik egy $\omega =\sqrt[]{2g/r}$ körfrekvenciájú, $A=v_0/\left(\omega r\right)$ maximális (szög)kitérésű harmonikus rezgőmozgás képletével, hiszen a $\begin{array}{c}{\displaystyle \phi \left(t\right)=A\text{sin}\omega t\mathrm{,}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mover accent="true"><mrow><mi>φ</mi></mrow><mo>˙</mo></mover></math>}\left(t\right)=A\omega \text{cos}\omega t}\end{array}$ (8) függvények nyilván kielégítik (7) egyenletet, továbbá a $\phi \left(0\right)=0$ és $\dot{\phi }\left(0\right)=v_0/r$ kezdeti feltételeket is. Az $X\left(t\right)$ függvény (5) és (8) felhasználásával számítható ki. $\begin{array}{c}{\displaystyle \dot{X}\left(t\right)=\frac{v_0}{2}\left(1-\text{cos}\omega t\right)\mathrm{,}}\end{array}$ ahonnan az egyenletes mozgás és a harmonikus rezgőmozgás ismert út‐sebesség képleteinek mintájára ($X\left(0\right)=0$ kezdeti feltételt is figyelembe véve) a végeredmény: $\begin{array}{c}{\displaystyle X\left(t\right)=\frac{v_{0}t}{2}-\frac{v_0}{2\omega }\text{sin}\omega t\mathrm{.}}\end{array}$  G. P.