Kezdőlap


Feladat:	3191. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1999/május, 307 - 309. oldal		PDF \| MathML
Témakör(ök):	Mozgási indukció, Térerősség és erő, Gauss-törvény, Mozgó elektromos töltésre ható erő (Lorentz-erő), Körmozgás (Tömegpont mozgásegyenlete), Feladat
Hivatkozás(ok):	Feladatok: 1998/október: 3191. fizika feladat

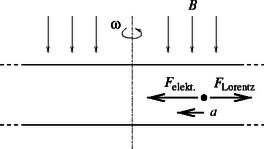
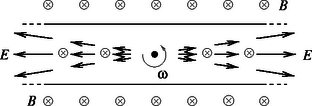
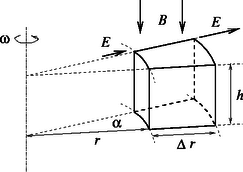
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fémrúd belsejében a töltéshordozók (az elektronok) szabadon el tudnak mozdulni. A mágneses térben mozgó rúd elektronjaira az érintőleges sebességükkel arányos nagyságú Lorentz-erő hat. Ennek hatására a rúd megforgatásakor az elektronok a rúdhoz képest elmozdulnak, a mágneses mező és a forgás irányától függően vagy kifelé, vagy a forgástengely felé mozognak. Kezdetben (a még nem forgó) a fémrúd belsejében nem volt elektromos erőtér, az elmozduló töltések hatására viszont egyre erősebb elektromos mező alakul ki, amely egyre jobban gátolja az elektronok további mozgását. A töltéshordozók átrendeződése mindaddig tart, amíg az elektromos erő és a mágneses Lorentz-erő együttes hatása éppen akkora nem lesz, amekkora erő az elektronok körpályán tartásához szükséges (1. ábra).
Jelöljük az elektron töltését $e$ -vel, tömegét pedig $m$ -mel, a mágneses indukció nagyságát pedig $B$ -vel! A forgástengelytől $r$ távolságban $r ω$ sebességgel mozgó elektronok gyorsulása $r ω^{2}$ , a mozgásegyenletük tehát

\begin{matrix} e E - e B r ω = - m r ω^{2}, \end{matrix}

ahol

E (r)

az elektromos tér nagysága a forgástengelytől

r

távolságban. Az elektromos mező nagysága tehát

\begin{matrix} E (r) = r (B ω - \frac{m}{e} ω^{2}), \end{matrix}

iránya pedig a forgástengelyre merőleges, hiszen mind a Lorentz-erő, mind pedig a centripetális gyorsulás ilyen irányú (vagy ezzel ellentétes).
Azt az eredményt kaptuk tehát, hogy a fém belsejében inhomogén elektromos mező alakul ki, melynek nagysága a forgástengelytől mért távolsággal egyenesen arányos (az arányossági tényezőt jelöljük

K

-val), iránya pedig (a szögsebesség és a mágneses mező irányától függően) a forgástengely felé, vagy éppen azzal ellentétesen mutat (2. ábra). Az elektron fajlagos töltése, vagyis az

e / m

hányados SI-egységekben mérve nagyon nagy szám, emiatt reális

B

és

ω

értékek mellett a körmozgáshoz szükséges erő sokkal kisebb, mint a Lorentz-erő, vagyis

K \approx B ω

.
Tekintsünk a fém belsejében egy kicsiny, trapéz alapú hasábbal közelíthető térrészt. Legyen az alaplap két ,,oldala''

r

és

r + Δ r

sugarú körív, másik két oldala zárjon be egymással

α

szöget, a magassága pedig legyen a forgástengellyel párhuzamos és

h

nagyságú (3. ábra). Számítsuk ki, mekkora elektromos fluxus halad át a térrész oldalfalain, majd ebből ‐ a Gauss-törvény felhasználásával ‐ számítsuk ki a vizsgált térrészben levő elektromos töltés mennyiségét!
Az

r

sugarú hengerpalást-darab területe

h r α,

a rajta áthaladó (belépő) elektromos fluxus tehát

E (r) \cdot h r α = h K α r^{2}

. A másik hengerpalást-darabon áthaladó (kilépő) fluxus

K h α {(r + Δ r)}^{2},

a többi felületen pedig nem haladnak át elektromos erővonalak, a fluxus nulla. A térrész teljes felületén összesen

\begin{matrix} Ψ = K h α [{(r + Δ r)}^{2} - r^{2}] \approx 2 K h α r Δ r \approx 2 B ω h α r Δ r \end{matrix}

fluxus halad át, s így Gauss törvénye értelmében a

Δ V

térfogatú térrészben

Q = ε_{0} Ψ

nagyságú (eredő) töltésnek kell elhelyezkednie. A térfogategységre jutó töltés nagysága, vagyis a töltéssűrűség:

\begin{matrix} ϱ = \frac{Q}{Δ V} = ε_{0} \frac{2 B ω h α r Δ r}{h r α Δ r} = 2 ε_{0} B ω . \end{matrix}

Ez a töltéssűrűség a helytől független, tehát a töltéseloszlás egyenletes. A kialakuló töltések előjele akkor pozitív, ha a Lorentz-erő a negatív elektronokat kifele ,,hajtja'', fordított forgásirány vagy fordított irányú mágneses tér esetében viszont a töltéseloszlás negatív lesz. Természetesen a test össztöltése mindkét esetben nulla kell legyen. A belülről hiányzó elektronok a rúd felületén (a hengerpaláston és a rúd végein) helyezkednek el, ha pedig a rúd belsejében eredő negatív töltéssűrűség alakul ki, akkor a felület pozitív lesz. A felületi töltéseloszlás pontos alakját elemi úton nem tudjuk meghatározni, de ez ebben a feladatban nem is volt kérdés.

(G. P.)

Megjegyzés. A töltéssűrűség kiszámításánál fontos volt, hogy a vékony fémrudat ne tekintsük ,,egydimenziós'' alakzatnak. Ha így tettünk volna, vagyis a kialakuló elektromos mezőnek csak a rúddal párhuzamos komponensét vizsgáljuk, akkor a fenti eredmény felét kapjuk csak meg. A hiba onnan származna, hogy ilyenkor nem vennénk figyelembe a rúd kicsiny (értelemszerűen hengeresnek tekintett) darabkájának palástján áthaladó elektromos fluxust. Meglepő, de igaz, hogy a majdnem párhuzamos elektromos mezőből éppen annyi elektromos fluxus ,,szökik meg'' a paláston, mint amennyi a henger alaplapján és fedőlapján átfutó fluxusok különbsége.