Kezdőlap


Feladat:	3192. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gáspár Merse Előd , Hegedűs Ákos , Katona Gergely , Kiss Gergely , Péterfalvi Csaba , Ravasz Mária- Magdolna , Terpai Tamás , Tóth Bálint
Füzet:	1999/április, 249 - 251. oldal		PDF \| MathML
Témakör(ök):	Tapadó súrlódás, Merev test egyensúlya, Merev test mozgásegyenletei, Feladat
Hivatkozás(ok):	Feladatok: 1998/október: 3192. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tételezzük fel először, hogy a tapadó súrlódás elegendően nagy (tehát a dominók sem egymáson, sem pedig a félhengeren csúsznak meg), és vizsgáljuk meg, hogy milyen erők hatnak a dominó-oszlop $α$ szöggel kibillent helyzetében. Az 1. ábrán látható jelöléseket használva állíthatjuk, hogy $T E$ megegyezik az $E F$ ív hosszával, azaz $R α$ -val, hiszen a dominók tisztán gördülnek a félhengeren. Stabil billegés akkor alakulhat ki, ha az $n$ dominóból álló merev test $K$ tömegközéppontban ható nehézségi erő hatásvonala az $E$ érintkezési ponttól balra esik, vagyis teljesül az

\begin{matrix} \frac{n d}{2} tg α = K T \cdot tg α < T E = R α, \end{matrix}

vagy az ezzel egyenértékű

\begin{matrix} n < \frac{2 R}{d} \cdot \frac{α}{tg α} < \frac{2 R}{d} = 12 \end{matrix}

feltétel. Eszerint 11 dominóból álló oszlopot rakhatunk fel félhenger tetejére, ha stabil billegést akarunk létrehozni. (Ha

α

elegendően kicsi, akkor

α \approx tg α

, tehát ilyenkor ‐ nem túl nagy szögkitérések esetén ‐ valóban fennáll a fenti egyenlőtlenség.)
Másképp is érvelhetünk. A

K

tömegközéppont magassága ‐ avagy az ezzel arányos helyzeti energia ‐ a dominók vízszintes (

α = 0

) helyzetében kell legyen a legkisebb, innen kicsit kibillentve a rendszert a helyzeti energiának növekednie kell. (Ha

α

növekedtével csökkenne a helyzeti energia, akkor a mozgási energia egyre nagyobb lenne, s ez ellentmond a stabil billegés feltevésének.) A tömegközéppont magassága a félhenger alapsíkja felett

\begin{matrix} h (α) = R cos α + R α sin α + \frac{n d}{2} cos α \approx (R + \frac{n d}{2}) + α^{2} (\frac{R}{2} - \frac{n d}{4}) . \end{matrix}

(Felhasználtuk, hogy kicsiny szögekre

sin α \approx α

és

cos α \approx 1 - α^{2} / 2

.) Látható, hogy a rendszer helyzeti energiájának akkor lesz minimuma

α = 0

-nál, ha

n < 2 R / d = 12

, vagyis legfeljebb 11 dominót rakhatunk egymásra, ha periodikusan billegő mozgást akarunk létrehozni.
Foglalkozzunk most egyetlen dominó megcsúszásának problémájával! Vegyük fel a dominó

α

szöggel kibillentett helyzetében a testre ható erőket (2. ábra), majd írjuk fel a mozgásegyenleteket! A test tömegközéppontjának koordinátái:

\begin{matrix} \begin{matrix} x = R sin α - R α cos α + \frac{d}{2} sin α \approx \frac{d}{2} α, \\ y = \frac{d}{2} cos α + R α sin α - R (1 - cos α) \approx R + \frac{d}{2} . \end{matrix} \end{matrix}

(Ismét alkalmaztuk a kicsiny szögek szögfüggvényeire vonatkozó közelítő formulákat, továbbá

α

négyzetét és magasabb hatványait elhanyagoltuk.)
A mozgásegyenletek:

\begin{matrix} \begin{matrix} N sin α - S cos α = m a_{x}, \\ m g - N cos α - S sin α = m a_{y}, \\ S \frac{d}{2} - N R α = Θ β, \end{matrix} \end{matrix}

ahol

Θ

a dominó tehetetlenségi nyomatéka a tömegközéppontján átmenő tengelyre vonatkoztatva,

β

pedig a szöggyorsulása. (Mivel

d ≪ R

, a dominót tekinthetjük vékony lemeznek, melyre a rúdhoz hasonlóan

Θ \approx \frac{1}{3} m R^{2} .

)
A mozgásegyenletekben is közelítve a szögfüggvényeket és tömegközépponti koordináták, valamint a szögelfordulás közötti kapcsolatot kihasználva a következő egyenleteket kapjuk:

\begin{matrix} \begin{matrix} N α - S = m \frac{d}{2} β, \\ N - m g = 0, \\ S \frac{d}{2} - N R α = \frac{1}{3} m R^{2} β . \end{matrix} \end{matrix}

Az egyenletrendszert megoldva megkaphatjuk a szöggyorsulás és a szögkitérés kapcsolatát:

\begin{matrix} β = - α \cdot \frac{3 g}{R^{2}} (R - \frac{d}{2}) . \end{matrix}

Stabil harmonikus rezgés akkor jöhet létre, ha a zárójelben álló kifejezés pozitív, vagyis ha

d < 2 R

. (Ez a megadott számértékekkel nyilván teljesül, de ha

d

helyébe

n d

-t írunk, megkapjuk az

n

darab dominó rezgésének korábban meghatározott

n < 2 R / d

feltételét is.)
A mozgásegyenletek fenti közelítő alakjából kiszámíthatjuk az

S

súrlódási erőt, az

N

nyomóerőt, majd ezek segítségével a megcsúszás elkerülésének feltételét is:

\begin{matrix} S (α) \approx m g α (1 + \frac{3 d}{2 R}) < μ N \approx μ m g . \end{matrix}

Látható, hogy

α

növekedtével

S

is növekszik, az

N

nyomóerő pedig gyakorlatilag változatlan (nevezetesen az

m g

-vel egyezik meg), emiatt a csúszásmentes gördülés feltétele a legnagyobb szögkitérésnél a leginkább kritikus. Ez a maximális szögkitérés

\begin{matrix} α_{max} < μ {(1 + \frac{3 d}{2 R})}^{- 1} \approx 0, 08, \end{matrix}

ami fokokra átszámítva kb.

4, 6^{\circ}

-nak felel meg.

Több dolgozat alapján

Megjegyzések. 1. A legnagyobb kitérésre adódó szög viszonylag kicsiny számértéke utólag ,,megerősíti'' a számolás során alkalmazott közelítések jogosságát (vagy legalább azt mutatja, hogy nincs ellentmondás az alkalmazott közelítés és a kapott végeredmény között). Néhányan kevesebb közelítéssel éltek, és a viszonylag bonyolult formulákat numerikusan vagy grafikusan értékelték ki. Ők a kitérés felső korlátjára

4, 61^{\circ}

-ot kaptak.
2. Sokan ‐ tévesen ‐ azt állították, hogy az

α

szögben kibillentett dominó lényegében egy

α

szögű lejtőn ,,érzi magát'', és azon a megcsúszás határszögének ismert

μ = tg α

képletéből

α < arc tg μ = 5, 7^{\circ}

-ot kaptak. Ebben a gondolatmenetben ott a hiba, hogy nem veszi figyelembe a sztatikus helyzet és a gyorsuló mozgás közötti különbséget. A dominó tömegközépontja ‐ közelítőleg ‐ harmonikus rezgőmozgást végez, a szélső helyzetben tehát van gyorsulása (sőt mi több, ott a legnagyobb a gyorsulása!), emiatt a súrlódási erőnek nem csak a súlyerő megfelelő komponensével kell egyensúlyt tartania, hanem a gyorsításhoz szükséges ,,többletet'' is fedeznie kell.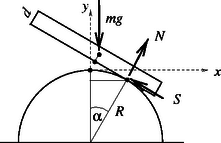