Kezdőlap


Feladat:	1521. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1975/május, 193 - 200. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Terület, felszín, Négyzetek, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/március: 1521. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot tavaly márciusban tűztük ki, és én csak akkor tudtam meg, hogy hibás, amikor a kezembe került az anyag nálunk szokásos (sajnos, igen lassú) forgása szerint az ún. ,,mintamegoldás'' (amit a dolgozatok kiértékelője ír a legjobb dolgozatok alapján).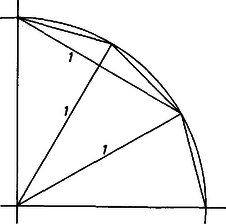
Ekkor kezdtem el foglalkozni a feladattal, és hadd mondjam most el az egészet abban a sorrendben, ahogy történt. Úgy érzem ugyanis, hogy ebben az esetben is fontosabb az eredménynél maga az az út, amelyen eljuthatunk hozzá, és én épp ezt az utat szeretném megmutatni. Az eredeti kitűzés szövege ez volt:
Egy $a$ oldalú négyzet csúcsai rajta vannak egy $t$ területű konvex sokszög határvonalán. Bizonyítsuk be, hogy a sokszög tartalmaz egy legalább $t / a$ hosszúságú szakaszt.
Szóval, ha még a sokszög átmérőjét ‐ azaz két egymástól legtávolabbi csúcsának távolságát ‐ $d$ -vel jelöljük, akkor az állítás szerint a

\begin{matrix} λ = \frac{t}{a d} \end{matrix}

hányados értéke legfeljebb 1. ‐ Érkezett 112 dolgozat, ezek közül 90 jó ellenpéldát ad az állításra, a többi 22 dolgozat hibás. Az utóbbiak szerzője vagy ,,bebizonyítja'' az állítást, vagy rossz ellenpéldát ad meg. A jó megoldások közül a feldolgozó hiányosnak mondta azokat, amelyek a kört hozták fel ellenpéldának, hiszen a feladatban sokszögről van szó. Ha mégis kiterjesztjük a vizsgálatunkat tetszőleges konvex görbére, akkor kétségtelenül a kör a legegyszerűbb ellenpélda. Ha ugyanis a sugár egységnyi, akkor

t = π

a = \sqrt[]{2}

d = 2

, tehát

\begin{matrix} λ_{kör} = \frac{π}{\sqrt[]{8}} = 1, 11. \end{matrix}

Konvex sokszögek körében a legegyszerűbb ellenpéldát a szabályos 12-szög adja (1. ábra): ha most is a körülírható kör sugarát választjuk egységnek, és a sokszöget 12 cikkre vágjuk, e cikkek közül két szomszédos együtt olyan négyszöget ad, amelyiknek az átlói merőlegesek egymásra, egységnyiek, tehát két cikk területe 1/2, így

t = 3

, és

a

és

d

ugyanannyi, mint az előbb:

\begin{matrix} λ_{12 - szög} = \frac{3}{\sqrt[]{8}} = 1, 06. \end{matrix}

1. ábra

Hasonlóan számolva a szabályos nyolcszögben

t

-re éppen

\sqrt[]{8}

-at kapunk, ez tehát látszólag már nem volna ellenpélda (2. ábra).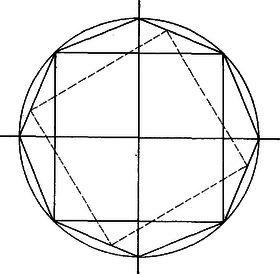

2. ábra

Vegyük észre azonban, hogy a nyolcszögünkbe nemcsak

\sqrt[]{2}

oldalú négyzetet írhatunk (amelynek csúcsai a nyolcszög csúcsai közül valók), hanem annál kisebbeket is, például olyat, amelynek a csúcsai: a nyolcszög minden második oldalfelező pontja. Ha pedig

t = \sqrt[]{8}

d = 2

, és

a < \sqrt[]{2}

, akkor

λ > 1

, tehát ‐ alkalmasan választott beírt négyzet mellett ‐ a szabályos nyolcszög is ellenpéldát ad. (Választhattunk volna a szabályos 12-szög esetében is ilyen, oldalfelezőpontokra támaszkodó beírt négyzetet, ebben az esetben

λ

még nagyobb volna, azonban a kör

λ

-jánál nem volna nagyobb.)
Tovább menve azt kapjuk, hogy még a szabályos ötszög is ad ellenpéldát: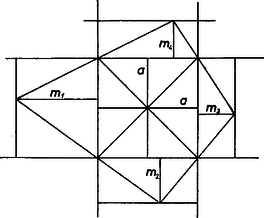

\begin{matrix} λ = \frac{5 - \sqrt[]{5}}{8} (1 + \sqrt[]{\frac{5 + \sqrt[]{5}}{2}}) = 1, 01. \end{matrix}

Viszont, ha a négyzet köré írt sokszög háromszög, akkor igaz az eredeti állítás, hiszen ‐ mivel csak három oldal áll rendelkezésünkre ‐ egy háromszögoldalon két négyzetcsúcs is van, és ha ezt az oldalt tekintjük alapnak, hosszát

b

-vel jelöljük, és a hozzá tartozó magasságot

m

-mel, akkor ‐ mint az könnyen látható ‐

\begin{matrix} \frac{1}{a} = \frac{1}{b} + \frac{1}{m}, \end{matrix}

és emiatt

\begin{matrix} λ = \frac{b m}{2 a d} = \frac{b + m}{2 d} = \frac{1}{2} (\frac{b}{d} + \frac{m}{d}) < 1, \end{matrix}

hiszen

b \leq d

és

m < d

. Sőt még négyszögre is könnyen igazolható az állítás ‐ legalábbis abban az esetben, ha a négyszög mindegyik oldalán egy négyzetcsúcs van. Ekkor ugyanis a négyszög csúcsainak a négyzet oldalaitól mért távolságát rendre

m_{1}

-gyel,

m_{2}

-vel,

m_{3}

-mal,

m_{4}

-gyel jelölve, a 3. ábra szerint

\begin{matrix} 2 t = (m_{1} + m_{2} + m_{3} + m_{4}) a + 2 a^{2} = a (m_{1} + a + m_{3}) + a (m_{2} + a + m_{4}) \leq 2 a d, \end{matrix}

hiszen az első csúcsból a harmadikba menve, utunknak az átmetszett négyzetoldalakra merőleges vetülete

m_{1} + a + m_{3}

, tehát a két csúcs távolsága legalább ennyi, a négyszög átmérője viszont nyilván nem lehet kisebb e két csúcs távolságánál.

3. ábra

Tehát

m_{1} + a + m_{3} \leq d

, és hasonlóan kapjuk, hogy

m_{2} + a + m_{4} \leq d

.
Ennyi derült ki a dolgozatokból. Bántott a dolog, mert ha volt is rá példa, hogy hibás feladatot tűztünk ki, ezt most észrevehettük volna. De ha már kitűztük ezt a példát, szerettem volna tudni, hogy mi is az igazság ezzel a

λ

-faktorral kapcsolatban. Elkezdtem tehát három irányban tapogatózni:
a) hogyan lehet a négyszögre vonatkozó állítást bizonyítani abban az esetben, ha egy négyszögoldalon két négyzetcsúcs van (mert abban valahogy egy percig sem kételkedtem, hogy négyszögekre még nem lehet a

λ

értéke 1-nél nagyobb);
b) milyen ‐ tetszőleges konvex görbére érvényes ‐ felső becslés adható

λ

-ra (mert ha ilyet találok, legalább utólag tudom, mit kellett volna kitűzni);
c) igaz-e, hogy

λ

a körre maximális (mert hát valahogy megszokta az ember, hogy nagyon sok ilyen kérdésben a kör az extremális).
Ezek közül a b) kérdésre volt a legkönnyebb válaszolni: ha meghúzzuk a görbének a négyzetoldalakkal párhuzamos támaszegyeneseit (azaz a négyzet oldalait addig mozgatjuk, irányukat megtartva, amíg még van közös pontjuk a konvex görbével), és ezeknek a négyzetoldalaktól mért távolságait rendre

m_{1}

-gyel,

m_{2}

-vel,

m_{3}

-mal,

m_{4}

-gyel jelöljük, akkor a konvex idomnak a négyzetből kilógó részeit egy-egy téglalapba foglaltuk be, és e részek területét becsülhetjük a téglalapok területével (4. ábra):

4. ábra

\begin{matrix} t \leq (m_{1} + m_{2} + m_{3} + m_{4}) a + a^{2} = a (m_{1} + a + m_{3}) + a (m_{2} + a + m_{4}) - a^{2} \leq \\ \leq 2 a d - a^{2} = (2 - \frac{a}{d}) a d, \end{matrix}

hiszen most is

m_{1} + a + m_{3} \leq d

és

m_{2} + a + m_{4} \leq d

, tehát tetszőleges konvex görbére igaz, hogy

\begin{matrix} λ = \frac{t}{a d} \leq 2 - \frac{a}{d} . \end{matrix}

Azt is aránylag könnyen lehet látni, hogy ha

d

túl nagy, mondjuk

d \geq 3 a

, akkor

λ \leq 1

, tehát a még tisztázatlan

d < 3 a

esetben egyenlőtlenségünk tovább javítható, ha benne

d

helyére

3 a

-t írunk; így kapjuk, hogy

λ \leq 5 / 3

. Valószínűleg még ez is tovább javítható, az viszont világos volt előttem, hogy ezen az úton soha el nem jutok a körig (még ha bizonyos ,,hevenyészett'' meggondolások alapján a

λ \leq 1, 17

egyenlőtlenség sem látszott bizonyíthatatlannak). Na jó, mondtam magamnak, a c) kérdés számomra túl nehéz, de legalább az a)-ra illene válaszolnom. Elkezdtem tehát a négyszögre még tisztázatlan másik két esetet számolni (5. ábra), és számoltam körülbelül egy hónapon át.

5. ábra

Ördög tudja miért, minden kézzelfogható eredmény nélkül. Ez viszont már határozottan bosszantott. Bánatomban elmeséltem mindenkinek a dolgot, akivel csak találkoztam. Köztük Vincze Istvánnak is, akivel a Matematikai Kutató Intézetben dolgozom együtt. Ö mondta nekem: lehet, hogy sok mindent próbáltál már, de az, hogy szimmetrizálj, még biztosan nem jutott eszedbe. Pedig, nézd csak, ha van két párhuzamos szakaszod, és eltolod őket úgy, hogy szimmetrikusak legyenek, akkor az átmérő kisebb lesz. Sok esetet tudok, amikor ez a szimmetrizálás volt a megoldás kulcsa. Ezek közül talán a leghíresebb az izoperimetrikus probléma, amiről Dörrie ,,A diadalmas matematika'' című könyvében is olvashatsz.
Erre valóban nem gondoltam. És csakugyan, ha

A B

C D

voltak az eredeti szakaszok, és csúcsaikat e körüljárás szerint bejárva kapunk konvex trapézt, továbbá

A C \leq B D

, akkor abban az egyenlő szárú

A_{1} B_{1} C_{1} D_{1}

trapézban, amelyben

A_{1} B_{1} = A B

C_{1} D_{1} = C D

és

A_{1}

B_{1}

A B

egyenesen,

C_{1}

D_{1}

C D

egyenesen van (6. ábra):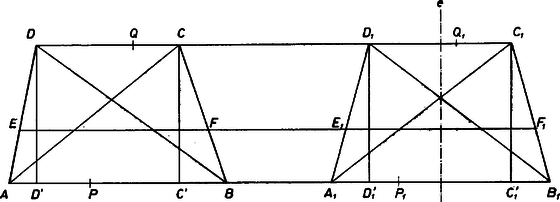

6. ábra

\begin{matrix} A C \leq A_{1} C_{1} = B_{1} D_{1} \leq B D, \end{matrix}

hiszen a

C

D

C_{1}

D_{1}

pontoknak az

A B

egyenesen levő vetületét

C'

-vel,

D'

-vel,

C'_{1}

-vel,

D'_{1}

-vel jelölve

\begin{matrix} A C' \leq A_{1} C'_{1} = \frac{A C' + B D'}{2} = B_{1} D'_{1} \leq B D', \end{matrix}

és a vetületek négyzetéhez még hozzá kell adnunk az

A B, C D

egyenesek távolságának a négyzetét, hogy az eredeti átlók négyzetét kapjuk.
Végezzük el ennek alapján a négyzet köré írt sokszögön a következő ‐ szimmetrizálásnak nevezett ‐ átalakítást (7. ábra).

7. ábra

Legyen

e

a négyzetnek egyik oldalával párhuzamos szimmetriatengelye, és vágjuk szét trapézokra a négyzet köré írt sokszöget a csúcsain átmenő,

e

-re merőleges egyenesekkel (a két szélen esetleg keletkező háromszögeket tekintsük az egyöntetűség kedvéért olyan trapéznak, amelynek két csúcsa azonos). Toljuk el e trapézok

e

-re merőleges oldalait

e

-re merőleges irányban úgy, hogy új helyzetükben

e

-re szimmetrikusak legyenek, és tekintsük az új szakaszok által meghatározott, egyenlő szárú trapézokból összerakható sokszöget. Megmutatjuk, hogy

α

) az új sokszög is konvex,

β

) a területe egyenlő az eredeti sokszög területével,

γ

) az átmérője az eredeti átmérőnél kisebb, esetleg egyenlő vele, és

δ

) a négyzet csúcsai az új sokszög határvonalán is rajta vannak.

Ha ugyanis

A B C D

a szétvágással keletkezett trapézok egyike, és

E

A D

egyenes tetszőleges pontja,

F

pedig az

E

-n átmenő,

A B

-vel párhuzamos egyenesnek

B C

-n levő pontja (6. ábra), akkor

E F

eltoltja az

E

-n átmenő,

A B

-vel párhuzamos egyenesnek

A_{1} D_{1}

B_{1} C_{1}

közti

E_{1} F_{1}

szakasza. Ha már

E F

szimmetrikus volt

e

-re, akkor

E_{1}

azonos

E

-vel,

F_{1}

pedig

F

-fel. Így van ez, ha

E F

a négyzet

e

-re merőleges oldala, tehát a négyzet csúcsai az új sokszögvonalon is rajta lesznek. (Ezzel beláttuk a

δ

állítást.)
Az

A B C D

és

A_{1} B_{1} C_{1} D_{1}

trapézok területe egyenlő, tehát a sokszögek területe is egyenlő. (Ezzel beláttuk a

β

állítást.)
Legyen

P_{1}

és

Q_{1}

az új sokszög két belső pontja, és legyen most

A_{1} B_{1}

, illetve

C_{1} D_{1}

P_{1}

-en, illetve

Q_{1}

-en átmenő,

e

-re merőleges húr az új sokszögben,

A B p

C D

pedig az eredeti sokszögnek az

A_{1} B_{1}

C_{1} D_{1}

egyeneseken levő húrja. Az

A B C D

trapéz benne van az eredeti sokszögben, emiatt

A_{1} B_{1} C_{1} D_{1}

is része az új sokszögnek, hiszen tetszőleges,

A B

-vel párhuzamos

E F

húrt tartalmazó szakasz szimmetrizáltja tartalmazza

E F

szimmetrizáltját,

E_{1} F_{1}

-et. Emiatt

P_{1} Q_{1}

benne van az új sokszögben, ez tehát konvex. (Ez volt az a állításunk.)
Végül a még nem bizonyított

γ

állítás következik abból, hogy

P_{1} Q_{1} \leq A_{1} C_{1} \leq B D

miatt a

P_{1} Q_{1}

szakasz hossza nem lehet nagyobb, mint az eredeti sokszög valamely alkalmasan választott szakaszának a hossza. Ha tehát az eredeti sokszög területe

t

, átmérője

d

, és az újban ugyanezek az adatok

t_{1}

és

d_{1}

, akkor

t_{1} = t

és

d_{1} \leq d

, és így

\begin{matrix} λ = \frac{t}{a d} \leq \frac{t_{1}}{a d_{1}} = λ_{1} . \end{matrix}

Elég tehát az

e

-re szimmetrikus konvex sokszögeket vizsgálni.
Legyen

f

a négyzet

e

-re merőleges szimmetriatengelye. Ismételjük meg az eljárásunkat,

e

szerepére most

f

-et választva, az új sokszög

f

-re is szimmetrikus lesz, és

e

-re szimmetrikus marad. Ez azért van így, mert az

e

-re szimmetrikus sokszög

f

-re merőleges húrjainak

e

-re vonatkozó tükörképei ismét húrok, és ezek az

e

-re szimmetrikus húrpárok az

f

-re vonatkozó szimmetrizálás során úgy mozdulnak el, hogy közben

e

-re szimmetrikusak maradnak (8. ábra).

8. ábra

Elég tehát

e

-re is,

f

-re is szimmetrikus sokszögeket vizsgálni ‐ ezek viszont centrálszimmetrikusak, centrumuk

e

és

f

metszéspontja, a négyzet

O

centruma. Ekkor viszont a sokszög átmérője akkor és csakis akkor

d

, ha benne van az

O

körüli,

r = d / 2

sugarú körben, és e körön is van csúcsa. Ha most a négyzet oldalát választjuk egységnek, akkor nyilván

d \geq \sqrt[]{2}

. Ha

d = \sqrt[]{2}

, a sokszög benne van a négyzet köré írható körben, és így

t \leq \frac{π}{2}

\begin{matrix} λ \leq \frac{π}{\sqrt[]{8}}; \end{matrix}

A kör tehát valóban extremális ‐ ha

d = \sqrt[]{2}

. Ha azonban

d > \sqrt[]{2}

, akkor

λ

értéke még nagyobb lehet. Írjunk például szabályos 12-szöget a négyzet köré úgy, hogy a négyzet csúcsai oldalfelezőpontok legyenek. Ekkor ugyan

d = 4 \sqrt[]{1 - \frac{\sqrt[]{3}}{2}}

t = \frac{3}{4} d^{2}

, és így ‐ mint már említettük ‐

λ

még nem lépi túl

λ_{kör}

értékét.

9. ábra

Ha viszont a 12-szög köré írható körnek a 12-szög

e

és

f

tengelyekhez csatlakozó oldalai feletti ívein újabb csúcsokat veszünk fel (9. ábra),

t

tovább nő, egészen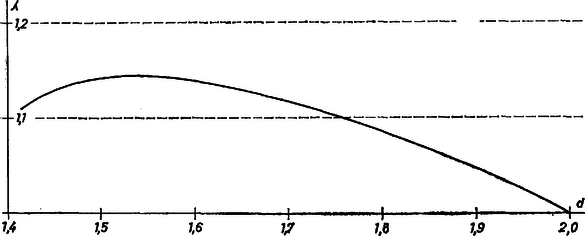

\begin{matrix} t = \frac{1}{3} \cdot \frac{3}{4} d^{2} + \frac{2}{3} \cdot \frac{π}{4} d^{2} = \frac{3 + 2 π}{12} d^{2} \end{matrix}

értékig, és ekkor már

\begin{matrix} λ = \frac{t}{a d} = \frac{3 + 2 π}{12} d = (1 + \frac{2 π}{3}) \sqrt[]{1 - \frac{\sqrt[]{3}}{2}} = 1, 13, \end{matrix}

ami nagyobb, mint a kör

λ

-ja. Belátható, hogy emellett a

d

mellett ez a

λ

maximális, és hogy

\sqrt[]{2} < d < 2

mellett hasonlóan kapjuk az extremális elrendezést. A megfelelő

λ

értékeket a 10. ábra mutatja, amelyről leolvasható, hogy a maximális

λ

két tizedesre

1, 14

. Ha azonban

d \geq 2

, akkor mindjárt belátjuk, hogy

λ \leq 1

10. ábra

Legyen ugyanis a négyzet egyik csúcsa

A

, a sokszög

A

-n átmenő oldalának egyenese (vagy ezek egyike)

g

, és messe

g

e

f

egyeneseket

E

-ben és

F

-ben. Könnyen látható, hogy (11. ábra)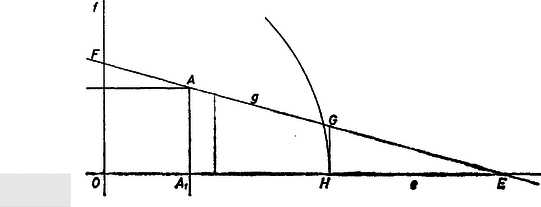

\begin{matrix} \frac{1}{O E} + \frac{1}{O F} = 2, \end{matrix}

ezért ha

O F \leq O E

, akkor

O F \leq 1 \leq O E

, tehát

O F \leq d / 2

F

d / 2

sugarú körön belül van.

11. ábra

O E \leq d / 2

, akkor

\begin{matrix} t \leq 4 t_{O E F} \leq 2 O E \cdot O F \leq d, \end{matrix}

tehát

λ \leq 1

(a négyzet oldala,

a

még mindig egységnyi), ha pedig

O E > d / 2

, legyen a

d / 2

sugarú körnek

O E

-n levő pontja

H

, a

H

-ban

e

-re emelt merőleges messe

E F

-et

G

-ben, akkor az

O H

szakasz felezőpontja

d / 2 > 1 / 2

miatt már a négyzeten kívül van, tehát az

O F G H

trapéz középvonala kisebb

1 / 2

-nél, és így

\begin{matrix} t \leq 4 t_{O F G H} = 4 \frac{O F + G H}{2} \cdot O H \leq 4 \cdot \frac{1}{2} \cdot \frac{d}{2} = d, \end{matrix}

tehát ismét azt kapjuk, hogy

λ \leq 1

.
Ezzel a c) kérdésre már lényegében válaszoltunk, de az a) kérdés még mindig megoldatlan. Szóval ha a négyzet oldala 1, és ha

d \geq 2

, akkor általában sem lehet

λ

1-nél nagyobb. Mi van, ha

d < 2

? Legyenek a négyszög átlói

e

és

f

, az átlók közti szög

ω

. Ekkor

t = \frac{1}{2} e f sin ω \leq \frac{d^{2}}{2}

, ami viszont

d < 2

miatt kisebb, mint

d

, tehát a fentiek után már ez az eset sem okozott nehézséget.