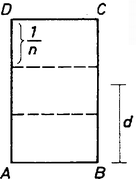|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A gyakorlat szövege a következő volt:
Daraboljuk fel egy szabályos hatszöget olyan részekre, melyekből négyzetet lehet összerakni.
Többen a megoldók közül így vélték megoldani a feladatot. Nyilván a két síkidom területe egyenlő. Vegyük a szabályos sokszög oldalát egységnyinek és számítsuk ki a területét: .
Ebből ki tudjuk számítani a négyzetoldalt, ami , s ezt meg tudjuk szerkeszteni pl. az alábbi módon (1. ábra). Az így rajzolt négyzet lesz megoldása a feladatnak.
 1. ábra
A feladat azonban nem ez volt !
A hatszöget véges számú olyan részre kellett szétvágni, amiből a négyzet összerakható. Ezt nevezzük átdarabolásnak.
Általában két sokszöget úgy darabolunk át egymásba, hogy mindkettőt felbontjuk véges számú részsokszögre úgy, hogy a részek kölcsönösen és egyértelműen egymáshoz rendelhetők, és az egymáshoz rendelt részek egybevágók.
Ebből és a területfüggvény tulajdonságából következik, hogy az egymásba darabolt sokszögnek a területe egyenlő.
Igaz az állítás megfordítása is, amit Bolyai Farkas tételeként szoktak idézni.
Az egyenlő területű sokszögek egymásba darabolhatók.
Van néhány közismert átdarabolási feladat. Azt például mindenki tudja, hogyan lehet egy háromszöget téglalappá átdarabolni.
1. Háromszög átdarabolása téglalappá.
 2. ábra
Húzzuk meg a háromszög valamelyik középvonalát, majd a szemközti csúcsból állítsunk merőlegest a középvonalra (2. ábra). Az I, ill. II-vel jelzett háromszögeket forgassuk el -kal. Az azonos számozású háromszögek egybevágóságából következik, hogy a téglalap területe egyenlő az eredeti háromszög területével. Ha a háromszög tompaszögű, az átdarabolást a 3. ábra mutatja.
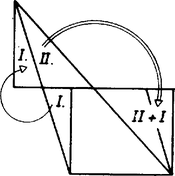 3. ábra
Ugyancsak közismert az is, hogyan lehet két egyenlő alapú és magasságú paralelogrammát átdarabolni egymásba.
2. Egyenlő alapú és magasságú paralelogrammák átdarabolása.
 4. ábra
A két bevonalkázott egybevágó háromszög áthelyezésével az egyik paralelogrammából eljuthatunk a másikba (4. ábra).
Nem ilyen egyszerű a megoldás, ha a csúcs a szakaszon kívülre esik.
Ekkor az és közös pontján át ‐ az és oldalakkal párhuzamos egyenesekkel ‐ az háromszöggel egybevágó háromszögekre bontjuk mindkét paralelogrammát. A háromszögek egybevágóságából azok (ill. a végén egy trapéz) áthelyezésével elvégezhetjük az átdarabolást (5. ábra).
 5. ábra
Most nézzünk néhány kevésbé ismert átdarabolási feladatot.
3. Minden téglalap átdarabolható olyan téglalappá, melynek egyik oldala adott.
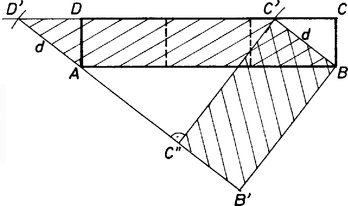
Tekintsük az téglalapot és a adott távolságot. Feltehető, hogy ; ha ugyanis lenne, akkor csökkentsük a téglalap oldalát a 6‐7. ábrán látható módon.
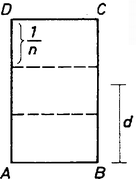 6. ábra
Messük el a egyenest a távolsággal -ből és -ból is ugyanabba az irányba (-től felé). A és háromszögek egybevágósága miatt az paralelogramma területe egyenlő az téglalap területével és így átdarabolhatók egymásba. Állítsunk -ből és -ből ( adott) merőlegeseket a egyenesre, a talppontok és . Állítjuk, hogy a kívánt téglalap. Egyik oldala , és az egybevágó és háromszögek révén az ábrából leolvashatjuk az átdarabolást. ( és , illetve és egyenlő alapú és magasságú paralelogrammák.) (7. ábra.)
 7. ábra
Ezek után térjünk vissza a C. 175. gyakorlat megoldására.
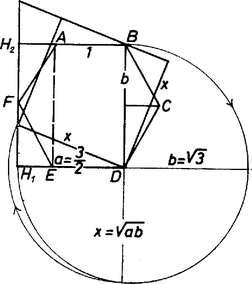 8. ábra
Jelöljük a hatszög csúcsait -fel. A 8. ábrán látható négy derékszögű háromszög nyilván egybevágó. A és háromszögeket áthelyezve az átló másik oldalára, az ábra szerint egy téglalaphoz jutunk. Az előbbiek szerint a téglalapot át tudjuk darabolni olyan téglalappá, melynek egyik oldala adott. Az adott oldal most annak a négyzetnek az oldala, amelynek területe egyenlő a téglalap területével. Ennek hosszát a téglalap oldalainak ismeretében már meg tudjuk szerkeszteni (pl. a derékszögű háromszögben ismert mértani középtétel segítségével).
Ha a téglalap oldalai és , a négyzet oldala .
(A beküldőktől elfogadtuk, ha csak a négyzetoldalt szerkesztették meg, de az átdarabolást már nem.)
Végezetül megemlítünk még néhány érdekes átdarabolási feladatot.
4. Minden konvex négyszög átdarabolható paralelogrammává.
Elegendő azt tudni, hogy a négyszög középvonalainak az oldalakkal való metszéspontjai paralelogrammát határoznak meg, a középvonalak tehát felezik egymást. Az átdarabolást a 9. ábra mutatja.
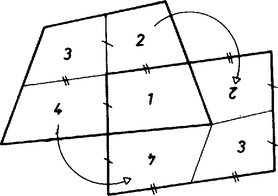 9. ábra
5. Kürschák Józseftől származik az sugarú körbe írt szabályos tizenkétszög átdarabolása három oldalú négyzetbe.
A 10. ábrán a tizenkétszög harmadrésze látható, az átdarabolást egy oldalú négyzetbe a 11. ábráról olvashatjuk le.
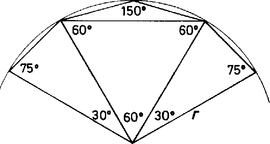 10. ábra
 11. ábra
Hasonló problémákat vethetünk fel testek (poliéderek) átdarabolásával kapcsolatban.
Néhány érdekes tétel:
Szabályos tetraéder nem darabolható át kockába.
A kockát nem lehet páronként különböző nagyságú kockákra szétvágni.
Megjegyzés. A megoldás során felhasználtuk Reiman István: Geometria és határterületei c. könyvének megfelelő részét. A könyvben még igen sok érdekes geometriai probléma található, melyeket olvasóink figyelmébe ajánlunk.
A területfüggvény minden síkidomhoz egy pozitív számot rendel (ez a területérték). Egybevágó sokszögekhez ugyanazt a területértéket rendeli, és ha a sokszöget részekre vágjuk, a részek területének összege egyenlő a sokszög területével. |
 PDF |
PDF |  MathML
MathML