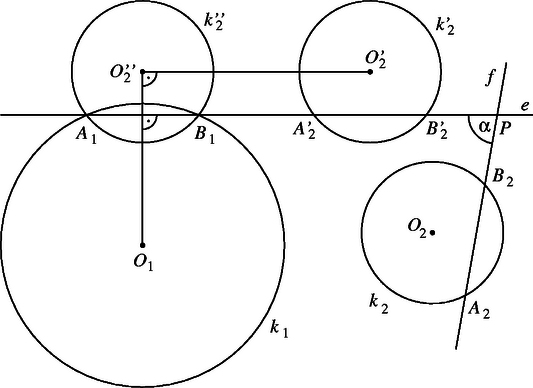
Tekintsük a feladatot megoldottnak. A $P$-n átmenő és egymással $\alpha$ szöget bezáró $e$ és $f$ egyenesek az adott $k_1$ és $k_2$ körökből az egyenlő hosszúságú $A_1{B}_1$ és $A_2{B}_2$ húrokat metszik ki (1. ábra). Forgassuk el $k_2$-t és $f$-et $P$ körül $\alpha$ szöggel úgy, hogy $f$ képe $e$ legyen. A $k_2$ képe legyen $k_2\text{'}$, $A_2$ és $B_2$ képe pedig $A_2\text{'}$, illetve $B_2\text{'}$. Ezzel problémánkat visszavezettük a következő, egyszerűbb feladatra: Adott két kör és egy pont. Szerkesszünk a ponton át olyan egyenest, amelyik a körökből egyenlő hosszúságú húrokat metsz ki. Eredeti feladatunk megoldásainak száma a módosított feladat megoldásszámától függ. Terjedelmi okokból a szokásos diszkussziótól el kell tekintenünk, ugyanis többféle bonyodalom adódhat.
Az 1. ábrán felvett helyzetben azért lesz megoldás, mert a $k_1$ és $k_2\text{'}$ körök $P$-ből vett látószögtartományainak van közös része, de egyik sem esik bele teljesen a másikba; $P$ körül forgatva a szelőt, az egyikből kimetszett húr hosszabbodik, a másik rövidül. Ismétlődne ez, ha $P$ e két kör ,,között'' lenne és emiatt egyik szögtartomány helyett csúcsszögtartományát néznénk. Valamivel nagyobb $\alpha$ esetén már nem lenne közös rész.
Más is okozhat gondot, pl. ha $k_2\text{'}$ metszené $k_1$-et, így csak akkor lehetne megoldás, ha közös húregyenesük éppen átmenne $P$-n. Előfordulhatna $r_1=r_2$ esetén, hogy a két kör azonos. Bele is eshetne $k_2\text{'}$ a $k_1$-be, ha $r_2<r_1$, másrészt esetleg ,,elnyelné'' azt, ha $r_2>r_1$.
Az $r_1=r_2$ esetben, ha $k_2\text{'}$ a $k_1$-en kívül esne, és $P$ ,,köztük'' volna,, gondolnunk kellene az $O_1{O}_2\text{'}$ egyenessel párhuzamos közös szelőre, és olyanra is, amely szétválasztja a két középpontot.
Visszatérve a feladat megoldására, toljuk el $k_2\text{'}$-t az $\overrightarrow{A_2\text{'}{A}_1}$ vektorral, a képét jelöljük $k_2\text{'}\text{'}$-vel. Mivel $A_1{B}_1=A_2{B}_2=A_2\text{'}{B}_2\text{'}$, ezért az eltolásnál $B_2\text{'}$ képe $B_1$ lesz. Jelöljük $O_1$, $O_2$, $O_2\text{'}$, $O_2\text{'}\text{'}$-vel a $k_1$, $k_2$, $k_2\text{'}$ és $k_2\text{'}\text{'}$ körök középpontját.
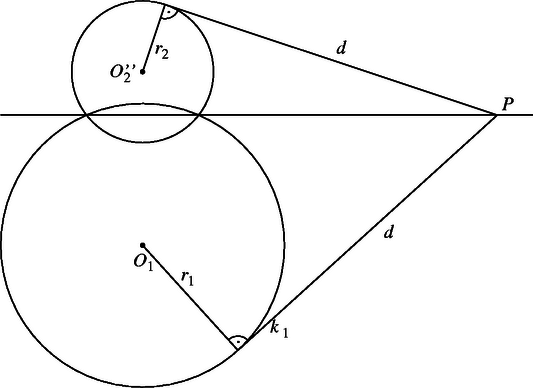
Az $e$ egyenes a $k_1$ és $k_2\text{'}\text{'}$ körök közös húrja, ezért $O_1{O}_2\text{'}\text{'}$ merőleges $e$-re. Viszont az eltolás miatt $O_2\text{'}{O}_2\text{'}\text{'}\parallel e$, tehát $O_2\text{'}{O}_2\text{'}\text{'}{O}_1\sphericalangle ={90}^{\circ }$, azaz $O_2\text{'}\text{'}$ rajta van az $O_1{O}_2\text{'}$ szakasz Thalész-körén. $P$-ből ‐ sőt az $e$ egyenes minden pontjából ‐ a $k_1$ és $k_2\text{'}\text{'}$ körökhöz egyenlő hosszúságú érintők húzhatók (ennek az állításnak a bizonyítása megtalálható pl. a Geometriai feladatok gyűjteménye I. kötetének 1323. feladatában). Jelöljük ennek az érintőnek a hosszát $d$-vel, $k_i$ sugarát pedig $r_i$-vel. Tudjuk, hogy az érintő merőleges az érintési pontban húzott sugárra, ezért Pitagorasz tétele szerint ${P{O}_2\text{'}\text{'}}^2=d^2+r_2^2$ és $P{O}_1^2=d^2+r_1^2$ (2. ábra). Vagyis $P{O}_2\text{'}\text{'}=P{O}_1^2-r_1^2+r_2^2$. Tehát $O_2\text{'}\text{'}$ rajta van a $P$ középpontú, $\sqrt[]{P{O}_1^2-r_1^2+r_2^2}$ sugarú körön.
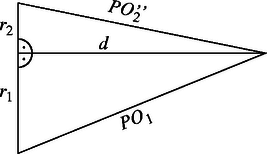
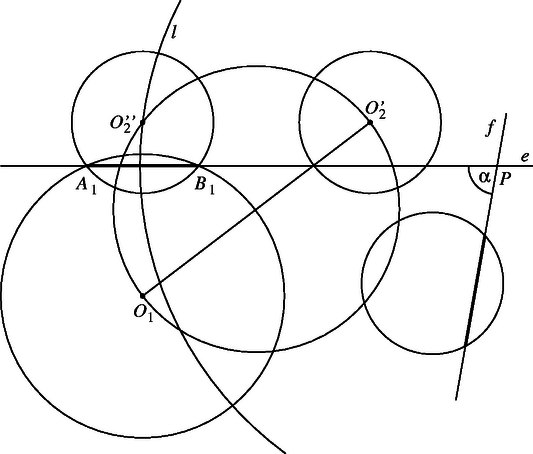
Ezek alapján a szerkesztést az alábbi módon végezhetjük: $P{O}_1$, $r_1$ és $r_2$ ismeretében megszerkesztjük a $\sqrt[]{P{O}_1^2-r_1^2+r_2^2}$ távolságot (3. ábra), majd ezzel a távolsággal mint sugárral $P$ körül kört rajzolunk. Jelöljük ezt a kört $l$-lel. $O_2$, $P$ és $\alpha$ segítségével megszerkesztjük $O_2\text{'}$-t. $O_1{O}_2\text{'}$ Thalész-körének és $l$-nek a metszéspontja adja $O_2\text{'}\text{'}$-t. Az $O_2\text{'}\text{'}$ körüli $r_2$ sugarú kör és $k_1$ metszéspontjai megadják a $P$-n átmenő $A_1{B}_1=e$ egyenest. Végül $e$-t $P$ körül $\alpha$ szöggel visszaforgatva (azaz az $O_{2}P{O}_2\text{'}\sphericalangle$ irányított szöggel ellentétes irányban forgatva ‐ 4. ábra) megkapjuk az $f$ egyenest. A szerkesztésből következik, hogy $e$ és $f$ a feladat feltételeinek megfelelő szelők.
A megoldások száma $O_2\text{'}\text{'}$-re 2, 1 vagy 0, attól függően, hogy $O_1{O}_2\text{'}$ Thalész-körének és $l$-nek hány közös pontja van. De az is kérdés, hogy a második az $O_2\text{'}\text{'}$ körüli $r_2$ sugarú kör metszi-e a $k_1$-et.