Először megmutatjuk, hogy az $e\text{'}$ egyenes mindig merőleges a gömb középpontja és $e$ által alkotott síkra.
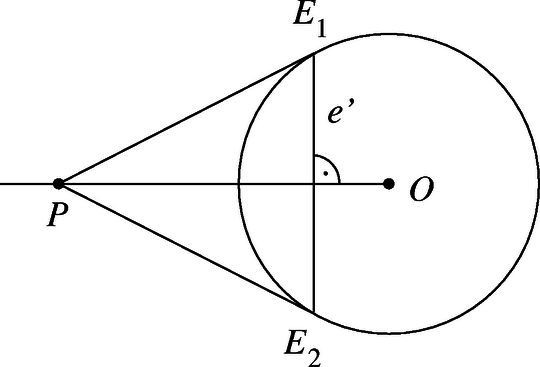
Jelöljük a gömb középpontját $O$-val. Az 1. ábrán $e$ merőleges a papírlap síkjára és azt $P$-ben metszi. Ha az $\left(O\mathrm{,}e\right)$ síkra tükrözzük az $e$-re illeszkedő egyik érintősíkot, akkor az $e$-re illeszkedő másik érintősíkot kapjuk, mert a tükrözésnél $e$-nek és a gömbnek a képe önmaga, érintősík képe pedig érintősík kell legyen. Ezért $E_1$ tükörképe $E_2$, tehát az $E_1{E}_2=e\text{'}$ egyenes merőleges az $\left(O\mathrm{,}e\right)$ síkra.
Ezért, ha $f$ és $g$ két olyan metsző egyenes, hogy $O$, $f$ és $g$ mind egy síkban vannak, akkor $f\text{'}$ és $g\text{'}$ egymástól különbözőek, és mindketen merőlegesek erre a síkra. Tehát ebben az esetben $f\text{'}$ és $g\text{'}$ párhuzamosak.
Ugyanezért, ha az $\left(O\mathrm{,}f\right)$ és $\left(O\mathrm{,}g\right)$ síkja egymástól különböző, $f\text{'}$ és $g\text{'}$ nem lehetnek párhuzamosak.
Megmutatjuk  viszont,
hogy $f\text{'}$ és $g\text{'}$ mindig egy síkban van.
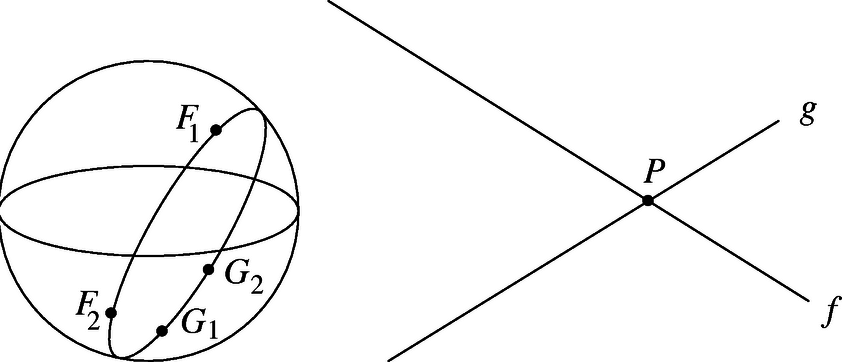
Legyen $f$ és $g$ metszéspontja $P$, az $f$-re, illetve $g$-re illeszkedő két-két érintősík és a gömb közös pontja pedig $F_1$, $F_2$, $G_1$ és $G_2$. Ekkor a $P{F}_1$, $P{F}_2$, $P{G}_1$ és $P{G}_2$ a gömbhöz $P$-ből húzott érintőegyenesek. Egy külső pontból egy gömbhöz húzott érintőegyenesek érintési pontjai a gömbön egy kört alkotnak, tehát egy síkban vannak. Azaz $F_1$, $F_2$, $G_1$ és $G_2$ egy síkban van, vagyis $f\text{'}$ és $g\text{'}$ is egy síkban van.
Összefoglalva: $f\text{'}$ és $g\text{'}$ mindig egy síkban van. Ha az $\left(f\mathrm{,}g\right)$ sík átmegy $O$-n, akkor $f\text{'}$ és $g\text{'}$ párhuzamos egyenesek, ha pedig az $\left(f\mathrm{,}g\right)$ sík nem tartalmazza $O$-t, akkor $f\text{'}$ és $g\text{'}$ szükségképpen metszik egymást,