Feladat: Gy.2953 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Csordás Péter ,  Elek Péter ,  ifj. Zsíros András ,  Kurucz Zoltán ,  Nyul Gábor ,  Rózsás Balázs ,  Terpai Tamás ,  Tóth Szabolcs ,  Varga Péter ,  Véber Miklós ,  Zubcsek Péter Pál 
Füzet: 1995/október, 407 - 409. oldal  PDF  |  MathML 
Témakör(ök): Szélsőérték-feladatok differenciálszámítás nélkül, Szöveges feladatok, Lineáris programozás, Gyakorlat
Hivatkozás(ok):Feladatok: 1994/december: Gy.2953

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük föl, hogy Ali Baba x font aranyat és y font gyémántot rak zsákjába. Határozzuk meg először, hogy ez milyen x és y esetén lehetséges. Összesen nem vihet el többet 100 fontnál, ezért

x+y≤100.
Nyilvánvaló, hogy x≥0, y≥0, hiszen csak nemnegatív mennyiségekről lehet szó. Még azt kell biztosítani, hogy a kincsek bele is férjenek a zsákba, azaz a térfogatuk sem lehet tetszőlegesen nagy, Ha gyémántból 40 font fér a zsákba, akkor 1 font gyémánt a zsák 140, y pedig az y40 részét tölti meg. Hasonlóan x font arany a zsák x200 részét tölti meg. A feltétel tehát
x200+y40≤1.
A lehetséges (x;y) számpárok ezek szerint az
F={(x;y):x≥0,y≥0,x+y≤100,x200+y40=1}
halmazt alkotják. Az F elemeinek megfelelő ponthalmazt koordináta-rendszerben is ábrázolhatjuk (1. ábra). A kapott alakzat egy ABCD négyszög, C csúcsának koordinátái legyenek x0, y0. Ezekre
x0+y0=100ésy040+x0200=1.
A második egyenletből x0=200-5y0, ezt az elsőbe írva 200-4y0=100, azaz y0=25 és x0=75.
Adott x, y esetén a kincsekért cserébe 20x+60y tevét adnak. Keressük tehát a bevonalkázott terület pontjai közül azt (vagy azokat), amely(ek)re 20x+60y (nevezzük ezt célfüggvénynek) értéke a lehető legnagyobb. Ezt úgy is megtehetjük, hogy meghatározzuk azt a legnagyobb c-t, amire még a
20x+60y=c(1)
egyenletnek van F-beli (x;y) megoldása. Ezt ugyanis elérheti a célfüggvény, nagyobbat már nem; a keresett x, y párt pedig (1) megoldása adja.
A 20x+60y=c egyenletű egyenesek közül néhányat berajzoltunk a 2. ábrába. Ezek egymással párhuzamosak, és c növelésekor a nyíllal jelölt irányba tolódnak el. A kérdés ezek szerint az, hogy meddig tolhatjuk ,,fölfelé'' az ilyen irányú egyeneseket úgy, hogy még legyen közös pontjuk F-fel. Nyilvánvaló, hogy ez a közös pont határesetben az F csúcsainak valamelyike lesz (előfordulhat, hogy van más közös pont is, de mindig található köztük csúcs). Elegendő tehát az A, B, C, D pontokban kiszámítani a célfüggvény értékét, s amelyiknél a legnagyobb, ahhoz tartozik a keresett c. Az A(0;0) pontra c=20x+60y=0; a B(100;0)-ra c=2000; C(75;25)-re c=3000; D(0;40)-re c=2400. A legjobb megoldás tehát 25 font gyémánt és 75 font arany, amiért 3000 tevét lehet kapni.
 ifj. Zsíros András (Nyíregyháza, Evang. Kossuth L. Gimn., I. o.t.) dolgozata alapján

 
Megjegyzés. Ellenőrizhető, hogy a (75;25) az egyedüli F-beli pont, amire c=3000. Ez a következő meggondolásból is látszik. Ha nem ez lenne az egyedüli pont, akkor a c=3000-hez tartozó ,,határhelyzetű'' egyenes F-et több pontban is metszené, ezek között lenne további csúcs is, ami ‐ mint a számokból látható ‐ lehetetlen.
Mindezekből leszűrhető a következő általános észrevétel. Ha egy lineáris célfüggvényt akarunk egy poliéderen maximalizálni, a maximumhelyet elég a csúcsok között keresni. Ha itt a maximum egyértelmű, akkor az a csúcs az egész halmazon is az egyetlen maximumhely.
Ha nem az, akkor látható, hogy a maximumot jelentő csúcsok által alkotott lap valamennyi pontja maximumhely. Ugyanez persze minimumfeladatnál is igaz. Ez a kérdéskör a lineáris programozás elméletéhez tartozik.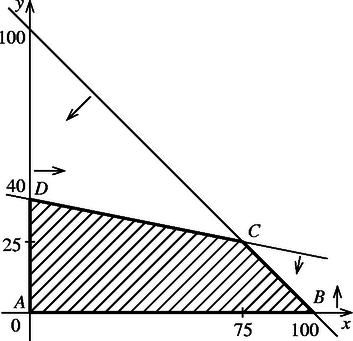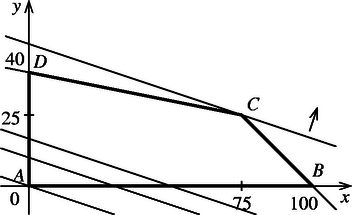