Feladat:	F.3037	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Endrődi Csilla ,  Farkas Illés ,  Farkas Péter ,  Galácz Ábel ,  Kardkovács Zsolt Tivadar ,  Krajcsovicz Éva ,  Lovász Zoltán ,  Molnár László ,  Sánta Zsuzsa
Füzet:	1995/május, 280 - 282. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Terület, felszín, Hatványközepek közötti egyenlőtlenség, Szélsőérték-feladatok differenciálszámítás nélkül, Körök, Thalesz tétel és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 1994/november: F.3037

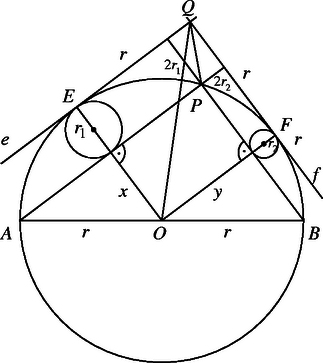
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Használjuk az ábra jelöléseit. Legyen a körszeletekbe írt körök területe $t_1$, ill. $t_2$. Thalész tétele szerint $x^2+y^2=r^2$. Ezt felhasználva $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle t_1+t_2=\pi \left(r_1^2+r_2^2\right)=}\\ \hfill {\displaystyle =\pi \left[{\left(\frac{r-x}{2}\right)}^2+{\left(\frac{r-y}{2}\right)}^2\right]=}\\ \hfill {\displaystyle =\frac{\pi }{4}\left[2r^2+x^2+y^2-2r\left(x+y\right)\right]=}\\ \hfill {\displaystyle =\frac{\pi }{4}\left[3r^2-2r\left(x+y\right)\right]\mathrm{.}}\end{array}}}\end{array}$ A számtani és a négyzetes közép közötti egyenlőtlenség szerint $\begin{array}{c}{\displaystyle \frac{r}{\sqrt[]{2}}=\sqrt[]{\frac{x^2+y^2}{2}}\ge \frac{x+y}{2}\mathrm{,}}\end{array}$ (1) ezért $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\pi }{4}\left[3r^2-2r\left(x+y\right)\right]\ge }\\ \hfill {\displaystyle \ge \frac{\pi }{4}\left(3r^2-2r\cdot r\sqrt[]{2}\right)=}\\ \hfill {\displaystyle =\frac{r^2\cdot \pi }{4}\left(3-2\sqrt[]{2}\right)\mathrm{.}}\end{array}}}\end{array}$ Ebből láthatjuk, hogy a területösszeg $\frac{r^2\pi }{4}\left(3-2\sqrt[]{2}\right)$-nél nem lehet kisebb. Ezt az értéket föl is veszi, ha $x=y$, azaz ha $P$ felezi az $AB$ ívet. A háromszögegyenlőtlenség szerint $2x+2y>2r$ minden lehetséges $P$-re, ezért $t_1+t_2$-nek maximuma csak az elfajuló $2x+2y=2r$ esetben lehetne, amit a feladat szövege kizár. Maximum tehát nincs, csak legkisebb felső korlát: $t_1+t_2<\frac{r^2\pi }{4}$. Az elfajuló esetben $r_1=\frac{r}{2}$, $r_2=0$ vagy fordítva.  Farkas Péter (Budapest, Szent István Gimn., IV. o.t.) és    Lovász Zoltán (Bonyhád, Perczel Mór Közg., Szki., IV. o.t.) dolgozatai alapján   II. megoldás. Vegyük figyelembe, hogy egy kör területe ugyanakkor a legnagyobb vagy legkisebb, amikor a kerülete. Ezért $k_1+k_2=\pi \left(r-x+r-y\right)=\pi \left(2r-\left(x+y\right)\right)$ szélsőértékeit kereshetjük. A megoldást az (1) egyenlőtlenség alapján az I. megoldáshoz hasonlóan kapjuk.  Kardkovács Zsolt Tivadar (Budapest, Károlyi M. Gimn., IV. o.t.)   III. megoldás. Az ábrán az $AP$-vel párhuzamos $e$ érintő és a $BP$-vel párhuzamos $f$ érintő a $Q$ pontban metszi egymást. Nyilván az $EQF\sphericalangle ={90}^{\circ }$, tehát $Q$-ból az $AB$ átmérőjű kör ${90}^{\circ }$-os szögben látszik. Ezért $QE=QF=r$ állandó, de akkor $OQ$ is állandó. Az ábráról láthatjuk, hogy $P{Q}^2=4r_1^2+4r_2^2$, tehát $PQ$ ugyanakkor minimális, amikor $t_1+t_2$. Ez akkor és csak akkor következik be, ha $P$ illeszkedik $OQ$-ra, vagyis ha $P$ az $AB$ ív felezőpontja. Hasonlóan látható, hogy $PQ$ akkor (lenne) a legnagyobb, ha $PQ$ érinti a kört, azaz $P=F$ vagy $P=E$, vagyis $AP=0$ vagy $PB=0$.   Megjegyzések. 1. Lovász Zoltán megmutatta, hogy a két beírt kör területének összege akkor is az egyenlő szárú háromszög esetén lesz minimális, ha $AB$ helyett egy tetszőleges húrt veszünk. 2. Farkas Péter $P$ helyett a $P_1$, $P_2$, $\text{...}$, $P_n$ pontokkal $n+1$ részre osztotta az $AB$ félkörívet. Bebizonyította, hogy az így keletkezett $n+1$ körszeletbe írt maximális érintő körök területének összege akkor minimális, ha $A{P}_1=P_1{P}_2=\text{...}=P_{n}B$.