|
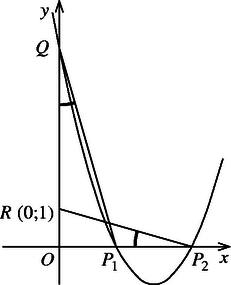
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megmutatjuk, hogy a közös pont az . A parabola tengelye párhuzamos az tengellyel, ezért a parabola azt csak egy pontban metszheti.
Ennek első koordinátája 0, így ha -val jelöljük, ez a pont .
Legyenek az tengellyel közös pontok
és . A feltételekből következik, hogy , , és . A gyökök és együtthatók közötti összefüggés szerint , azaz ahol a koordinátarendszer kezdőpontja.
(1)-ből következik, hogy ami azt jelenti, hogy , és ezért . Emiatt az szakasz a és a pontból ugyanakkora szögben látszik, tehát , , , egy körön vannak. Ábránk a esethez készült, de a bizonyítás ugyanígy működik, ha , amikor a parabola belső pontja.
| Braun Gábor (Budapest, Szent István Gimn., II. o.t.) |
|
 PDF |
PDF |  MathML
MathML