Feladat: Gy.2949 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Papp Ágnes 
Füzet: 1995/május, 278 - 279. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria térben, Gyakorlat
Hivatkozás(ok):Feladatok: 1994/november: Gy.2949

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először vizsgáljuk meg, hogy milyen lapjai lehetnek egy ötlapú testnek. A lapok között nem lehet ötszög vagy ötnél több oldalú sokszög, mert ha ilyen volna, akkor annak minden oldalához csatlakozna a testnek 1‐1 lapja, a lapok száma tehát legalább 1+5=6 lenne. Ezért minden lap háromszög vagy négyszög.
Jelöljük a háromszögek számát h-val, a négyszögek számát n-nel, a test éleinek számát e-vel, csúcsainak számát pedig c-vel. A test minden éle egyúttal két oldallapnak is oldaléle, ezért

2e=3h+4n.
Ebből következik, hogy a háromszöglapok száma h=2e-4n3=2⋅e-2n3, ami biztosan páros, mert h egész. Tehát csak h=0, 2 vagy 4 jön szóba, amiből sorra n=5, 3 vagy 1, így e=10, 9 vagy 8. A test minden csúcsában legalább 3 él találkozik, és minden élen pontosan 2 csúcs van, ezért c≤23e. Vagyis az egyes esetekben a csúcsok száma legfeljebb 6, 6, illetve 5. Vizsgáljuk meg a három lehetőséget.
(i) A testnek 5 négyszöglapja, 10 éle és legfeljebb 6 csúcsa van. Ekkor 3c<2e, ezért van olyan csúcs, amelyben legalább 4 él, s ezért legalább 4 lap találkozik. Jelöljük ezt a csúcsot A-val (1. ábra). Az A-t tartalmazó egyik négyszög további csúcsai legyenek B, C és D. Az AB élt egy ABCD-től különböző négyszöglap is tartalmazza, ennek további csúcsai legyenek E és F. E két csúcs nincs benne az ABCD síkban, ezért az A, B, C, D, E és F pontok a testnek 6 különböző csúcsát alkotják. Mivel a testnek legfeljebb 6 csúcsa lehet, azért a testnek az A-ból kiinduló negyedik ‐ azaz AB-től, AD-től és AF-től különböző ‐ élén nem lehet további csúcs. Ez nyilvánvalóan ellentmondás, ezért ilyen test nem létezik.
(ii) n=3, h=2 és e=9. Legyen ABCD és ABEF a test két szomszédos négyszöglapja (2. ábra). Mivel az öt lap közül három négyszög, azért ilyenek biztosan vannak. A testnek legfeljebb 6 csúcsa van, ezért nem lehet A, B, C, D, E, F-től különböző csúcsa. Ez azt jelenti, hogy a harmadik négyszöglap CDEF kell legyen. Tehát a test két háromszöglapja egymással nem szomszédos, a négyszöglapok mindegyike pedig szomszédos a két másik négyszöggel és a két háromszöggel. Ezért a testnek 9 lapszöge van.
Megmutatjuk, hogy a lapszögek között legfeljebb 7 derékszög lehet. 7 derékszög található egy derékszögű háromszög alapú egyenes hasáb lapszögei között (3. ábra), mert a három oldallap az alapra is és a fedőlapra is merőleges, az oldallapok egymással bezárt szögei pedig megegyeznek az alapháromszög szögeivel, tehát ezek között pontosan egy derékszög van. A lapszögek között 7-nél több derékszög nem lehet, mert akkor volna olyan háromszöglap, amelyre mind a három hozzá csatlakozó négyszög merőleges lenne, továbbá a négyszögek közül is legalább két pár egymásra merőleges lenne. De ebben az esetben a négyszöglapok egymással bezárt szögei definíció szerint megegyeznek a háromszöglap szögeivel, amelyek között nem lehet két derékszög.
(iii) n=1, h=4 és e=8. Ekkor a csúcsok száma 5, a test négyszög alapú gúla (4. ábra). Oldallapjai közül legfeljebb kettő lehet merőleges az alaplapra, mert ha három merőleges lenne, akkor azok metszésvonalai ‐ amelyek a gúla oldalélei ‐ egymással párhuzamosak lennének, hiszen merőlegesek volnának az alaplapra. Tehát a gúla 8 lapszöge közül legalább 2 nem derékszög, azaz a derékszögű lapszögek száma ebben az esetben kisebb, mint 7.
Ezzel beláttuk, hogy egy ötlapú test lapszögei közül legfeljebb 7 lehet derékszög.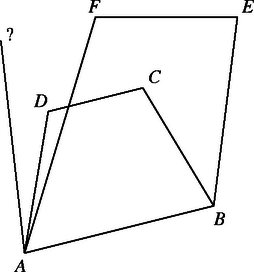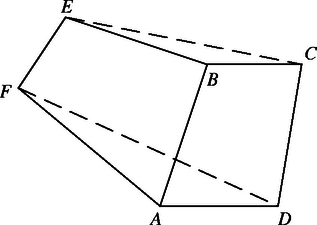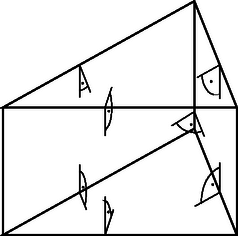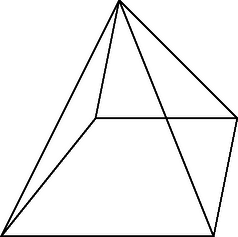