Kezdőlap


Feladat:	Gy.2948	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bérczi Gergely , Burcsi Péter , Fejes Tóth Péter , Fejős Ibolya , Makai Márton , Pap Gyula , Sánta Zsuzsa , Tóth Gábor Zsolt , Zubcsek Péter Pál
Füzet:	1995/május, 276 - 277. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Ponthalmazok, Derékszögű háromszögek geometriája, Egyéb ponthalmazok a koordinátasíkon, Gyakorlat
Hivatkozás(ok):	Feladatok: 1994/november: Gy.2948

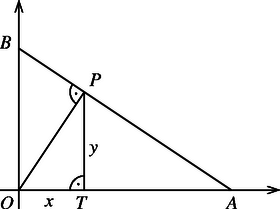
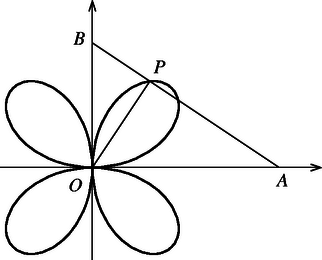
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nyilvánvaló, hogy a görbének csak egy pontja van a koordinátatengelyeken, az $O$ origó. Legyen $P (x, y)$ a görbének egy olyan pontja, amelyik egyik koordinátatengelyen sincs rajta. Az $O A$ -ra $P$ -ből állított merőleges talppontja legyen $T$ . Ekkor $O T = | x |$ és $P T = | y |$ .
Az $O P T$ , a $B O P$ és az $O A P$ háromszögek hasonlók, mert szögeik megegyeznek (mindhárom háromszög hasonló a $B O A$ háromszöghöz is). Ezért megfelelő oldalaik aránya is egyenlő:

\begin{matrix} \frac{O P}{P B} = \frac{P T}{O T} = \frac{| y |}{| x |} és \frac{O P}{A P} = \frac{O T}{P T} = \frac{| x |}{| y |} . \end{matrix}

Ezekből az egyenlőségekből kapjuk, hogy

\begin{matrix} | x | \cdot O P = | y | \cdot P B és | y | \cdot O P = | x | \cdot A P . \end{matrix}

Szorozzuk meg az első egyenlőséget

| x |

-kel, a másodikat

| y |

-kel, és ezután adjuk őket össze:

\begin{matrix} (x^{2} + y^{2}) O P = | x \cdot y | \cdot (A P + P B) . \end{matrix}

Pitagorasz tétele szerint

O P = \sqrt[]{x^{2} + y^{2}}

; feltételeink szerint

A P + P B = A B = 1

, ezeket behelyettesítve:

\begin{matrix} (x^{2} + y^{2}) \sqrt[]{x^{2} + y^{2}} = | x y | . \end{matrix}

Ez pontosan akkor teljesül, ha

\begin{matrix} {(x^{2} + y^{2})}^{3} = x^{2} \cdot y^{2} . \end{matrix}

(1)

Ezt az egyenletet az origó koordinátái is kielégítik, így megmutattuk, hogy a keresett görbének minden pontja rajta van az (1) egyenletű görbén.
Megmutatjuk, hogy ha egy

Q

pont koordinátái kielégítik az (1)
egyenletet, akkor az

A B

szakasznak van olyan helyzete, amelynél az origóból

A B

-re bocsátott merőleges talppontja éppen

Q

. Ha

Q

egyik koordinátája 0, akkor (1) miatt a másik is 0, az origó pedig nyilván előáll talppontként, pl. akkor, amikor

A (1; 0)

és

B (0; 0)

. Ha

Q (u; v)

, ahol

u \cdot v \neq 0

, akkor legyen

\begin{matrix} A (\frac{v}{\sqrt[]{u^{2} + v^{2}}}; 0) és B (0; \frac{u}{\sqrt[]{u^{2} + v^{2}}}) . \end{matrix}

Ekkor

A B

hossza Pitagorasz tétele alapján 1, és könnyen látható, hogy

O Q

merőleges

A B

-re.
Ezzel megmutattuk, hogy a keresett görbe egyenlete

\begin{matrix} {(x^{2} + y^{2})}^{3} = x^{2} + y^{2} . \end{matrix}

Pap Gyula (Debrecen, Fazekas M. Gimn., II. o.t.) dolgozata alapján