Feladat: Gy.2938 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Ács Róbert ,  Ádám Vera ,  Bárány Kristóf ,  Baumgartner Klaudia ,  Czirok Levente ,  Fazekas Borbála ,  Fejős Ibolya ,  Kiss László ,  Less Áron ,  Megyeri Csaba ,  Molnár-Sáska Balázs ,  Papp Eszter ,  Pintér Dömötör ,  Rózsás Balázs 
Füzet: 1995/május, 275 - 276. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Oldalfelező merőleges, Gyakorlat
Hivatkozás(ok):Feladatok: 1994/október: Gy.2938

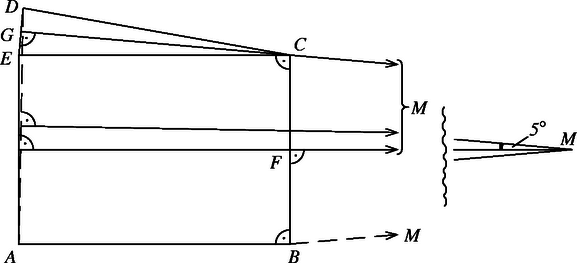
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen E az a pont, amelyre az ABCE négyszög téglalap. Ekkor AB=CE=DC és DCE∢=DCB∢-90∘=10∘ (1. ábra). Az AE szakasz felező merőlegese megegyezik BC felező merőlegesével, tehát M az AED háromszög köré írható körnek a középpontja. Ezért ED felező merőlegese is átmegy M-en. Viszont az EDC háromszög egyenlő szárú, ezért ED felező merőlegese egyúttal az ECD szög szögfelezője is, ami EC-vel 10∘2=5∘-os szöget zár be.
Jelöljük BC felezőpontját F-fel, ED felezőpontját G-vel. Ekkor CMF∢=GCE∢=5∘, mert CE‖MF; G, C és M pedig egy egyenesbe esik. A CMB háromszög is egyenlő szárú, ezért CMF∢=FMB∢, vagyis BMC∢=BMF∢+FMC∢=10∘.
 Jánosi Gergely (Budapest, Eötvös J. Gimn., I. o.t.) dolgozata alapján

 
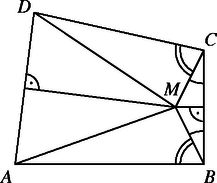
Megjegyzés. Sokan elkövették az alábbi hibát: ,,A 2. ábra jelöléseit használva: AM=MD, BM=MC és AB=CD, tehát az ABM és DCM háromszögek egybevágóak, ezért ABM∢=DCM∢. Másrészt a BMC háromszög egyenlő szárú, ezért MBC∢=MCB∢. Ezekből következik, hogy
90∘=ABC∢+MBC∢=DCM∢+MCB∢==DCB∢=100∘.
Ez ellentmondás.''
Ez a gondolatmenet azért hibás, mert a pontok a valóságban nem úgy helyezkednek el, ahogy az ábrán. A vázlat nem mérethű, DC<AB.