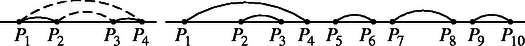|
| Feladat: |
Gy.2947 |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bérczi Gergely , Cseke Zsuzsa , Csordás Péter , Czirok Levente , Deli Tamás , Dulai Tibor , Fejős Ibolya , Fodor Bea , Frenkel Péter , Hangya Balázs , Juhász András , Katona Zsolt , Kiss László , Laczó Tibor , Less Áron , Lippner Gábor , Lőrincz Ildikó , Molnár-Sáska Balázs , Németh Balázs , Nyakas Péter , Nyul Gábor , Pap Gyula , Papp Beáta Andrea , Pintér Dömötör , Poór Judit , Reviczky Ágnes , Serény András , Simon Barna , Terpai Tamás , Varga Péter , Vincze László , Visontai Mirkó , Zubcsek Péter Pál |
| Füzet: |
1995/április,
216 - 217. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Gyakorlat |
| Hivatkozás(ok): | Feladatok: 1994/november: Gy.2947 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük -vel az összekötési lehetőségek számát abban az esetben, amikor a félsík határoló egyenesén pont van megadva. Feladatunk ekkor meghatározása. Az egyenesen valamelyik irányban haladva számozzuk meg a pontokat 1-től 10-ig. Két összekötött pont között nem lehet páratlan sok pont, mert akkor azokat nem tudnánk a feltételeknek megfelelően párokba állítani. Ezért -et úgy írhatjuk fel, hogy megkülönböztetjük azokat az eseteket, amikor az első pont a másodikkal, a negyedikkel, a hatodikkal, a nyolcadikkal vagy a tizedikkel van összekötve.
Ha az első a másodikkal van összekötve, akkor a többi nyolc pontot féleképpen állíthatjuk párba. Ha az első a negyedikkel van összekötve, akkor az 1. és a 4. pont között lévő pontok összekötési lehetőségeinek számát ‐ két összekötött pont között lévő pontok csak egymással köthetők össze ‐ kell szoroznunk a maradék hat pont összekötési lehetőségeinek számával: . Hasonló okoskodással a másik három esetben a lehetőségek száma , és . Tehát: | |
Ugyanígy kapjuk, hogy | |
Nyilvánvaló, hogy két pontot egyféleképpen lehet párba állítani, ezért . Ezt behelyettesítve , , és végül .
Tehát a párba állítási lehetőségek száma: 42.
Megjegyzés. Általában igaz, hogy . Ennek segítségével az is igazolható, hogy .
| Katona Zsolt (Fazekas M. Főv. Gyak. Gimn., I. o.t.) |
|
|
 PDF |
PDF |  MathML
MathML