Kezdőlap


Feladat:	Gy.2931	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Deli Tamás , Nyul Gábor , Treer Albert , Varga Haszonits István
Füzet:	1995/április, 203 - 204. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Körérintők, Diszkusszió, Gyakorlat
Hivatkozás(ok):	Feladatok: 1994/szeptember: Gy.2931

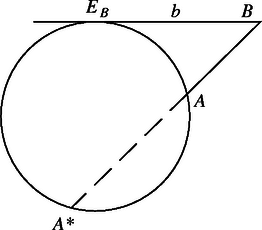
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatnak nyilván csak akkor van értelme, ha sem $A$ , sem $B$ nem esik a kör belsejébe. Ha $A$ és $B$ egyike sincs rajta a körvonalon, akkor az állítás igaz, egyébként pedig nem. Ha ugyanis $A$ a körvonalon, $B$ pedig a körön kívül van, akkor $a = 0$ , $b > A B$ , tehát $a + b > A B$ , viszont az $A B$ szakasznak van közös pontja $k$ -val, így ebben az esetben az állítás nem igaz (1. ábra).
Ha $A$ is és $B$ is a körön kívül helyezkedik el, akkor a következő három esetet kell megvizsgálnunk:

*	(i) $A B$ $k$ -n kívül helyezkedik el,

*	(ii) $A B$ egy $E$ pontban érinti $k$ -t,

*	(iii) $A B$ metszi $k$ -t.

A feladat állítása az, hogy az (i) esetben

a + b > A B

, míg a másik két esetben

a + b \leq A B

. Mindhárom esetben igaz, hogy az

A

-ból, illetve

B

-ből

k

-hoz húzható két-két érintőszakasz egyenlő hosszú, ezért mindig elegendő azt az érintőszakaszt vizsgálnunk, amelyik számunkra ,,kedvezőbb'' elhelyezkedésű.
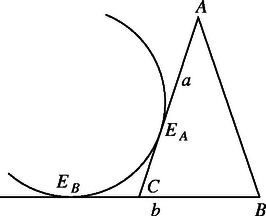
Az (i) esetben feltehetjük, hogy a két érintőegyenes közül az egyik elválasztja

A B

-t és

k

-t (tehát a kör, illetve a szakasz az érintőegyenes két különböző oldalára esik), a másik pedig nem. Ábránkon az

A

-ból húzott érintő az elválasztó. Ekkor a két érintőegyenes

C

metszéspontja a

B

-ből húzott érintőszakasz belső pontja lesz, de az

A

-ból húzottnak nem. A pontok a 2. ábrán látható módon fognak elhelyezkedni. Az ábra jelöléseit használva:

\begin{matrix} a + b = A E_{A} + B E_{B} = A E_{A} + C E_{B} + C B = A E_{A} + C E_{A} + C B = A C + C B . \end{matrix}

Viszont a háromszög-egyenlőtlenség miatt

A C + C B > A B

, tehát ebben az esetben igaz a feladat állítása.
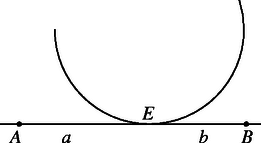
A (ii) esetben (3. ábra)

a + b = A E + E B = A B

, vagyis ekkor nyilván igaz az állítás.
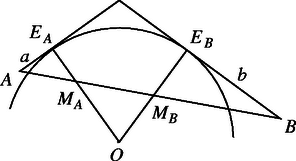
A (iii) esetben azokat az érintőket rajzoljuk meg, amelyek érintési pontjait

A B

elválasztja a

k

kör

O

középpontjától (4. ábra). Legyen az

E_{A} O

, illetve az

E_{B} O

sugárnak az

A B

-vel való metszéspontja

M_{A}

, illetve

M_{B}

. Ekkor az

A

M_{A}

M_{B}

B

pontok ebben a sorrendben helyezkednek el ‐

M_{A}

és

M_{B}

esetleg egybeesik, ha

O

rajta van

A B

-n ‐, ezért

a + b < A M_{A} + M_{B} B \leq A B

.
Ezzel beláttuk, hogy a feladat állítása pontosan akkor igaz, ha

A

is és

B

is a körön kívül helyezkedik el.

Nyul Gábor (Debrecen, Fazekas M. Gimn., I. o.t.) dolgozata alapján