Kezdőlap


Feladat:	F.3031	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Becker Johanna , Braun Gábor , Burcsi Péter , Elek Péter , Erdélyi László , Farkas Illés , Farkas Péter , Galácz Ábel , Gémes Tamás , Gerő Tamás Miklós , Gröller Ákos , Hegedűs Viktor , Kerekes Tamás , Király Csaba , Kovács Baldvin , Lolbert Tamás , Majlender Péter , Nagy Katalin , Németh Balázs , Németh Zoltán , Orbán András , Pap Gyula , Perényi Márton , Puskás Zsolt , Sági Krisztián , Sándor András , Sánta Zsuzsa , Somogyi Balázs , Szabó Dénes , Szailer Tamás , Szász Nóra , Szobonya László , Szőke Ervin , Torma Péter , Tóth Gábor Zsolt , Valkó Benedek , Véber Miklós
Füzet:	1995/március, 154 - 156. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságvonal, Magasságpont, Hatványközepek közötti egyenlőtlenség, Feladat
Hivatkozás(ok):	Feladatok: 1994/október: F.3031

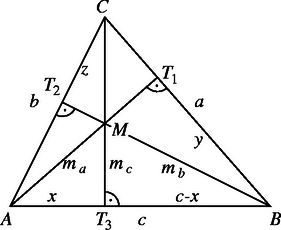
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először hegyesszögű háromszögre igazoljuk a feladat állítását. Az 1. ábra jelöléseit használva, az $A M T_{3}$ és az $A B T_{1}$ háromszögek hasonlósága alapján $A M : x = c : m_{a}$ , amiből

\begin{matrix} m_{a} \cdot A M = c \cdot x . \end{matrix}

(1)

Két ugyanilyen hasonlóságból

B M : y = a : m_{b}

és

C M : z = b : m_{c}

. Ezekből az összefüggésekből

\begin{matrix} m_{b} \cdot B M = a \cdot y és m_{c} \cdot C M = b \cdot z . \end{matrix}

(2)

A C T_{3}

és

B C T_{3}

derékszögű háromszögekből:

b^{2} - x^{2} = a^{2} - {(c - x)}^{2}

, amiből

x = \frac{b^{2} + c^{2} - a^{2}}{2 c}

. Hasonlóan kapjuk, hogy

y = \frac{a^{2} + c^{2} - b^{2}}{2 a}

és

z = \frac{a^{2} + b^{2} - c^{2}}{2 b}

. Az (1) és (2) alatti összefüggéseket összeadva, és

x

y

z

kifejezéseit fölhasználva:

\begin{matrix} \begin{matrix} m_{a} \cdot A M + m_{b} \cdot B M + m_{c} \cdot C M = \\ = c \cdot \frac{b^{2} + c^{2} - a^{2}}{2 c} + a \cdot \frac{a^{2} + c^{2} - b^{2}}{2 a} + b \cdot \frac{a^{2} + b^{2} - c^{2}}{2 b} = \frac{a^{2} + b^{2} + c^{2}}{2} . \end{matrix} \end{matrix}

Ezután azt kell bizonyítanunk, hogy

\begin{matrix} m_{a}^{2} + m_{b}^{2} + m_{c}^{2} \leq \frac{3}{4} (a^{2} + b^{2} + c^{2}) . \end{matrix}

(3)

A (3) egyenlőtlenség következik az F. 2972. feladat állításából, ami így szól:

m_{a}^{2} + m_{b}^{2} + m_{c}^{2} \leq s^{2}

, ahol

s = \frac{a + b + c}{2}

. Megoldásai megtalálhatók lapunk 1994/4. számában. Mindössze annyit kell megmutatnunk, hogy

\begin{matrix} {(\frac{a + b + c}{2})}^{2} \leq \frac{3}{4} (a^{2} + b^{2} + c^{2}) . \end{matrix}

Ez pedig nyilvánvaló, mert ekvivalens az

\begin{matrix} \frac{a + b + c}{3} \leq \sqrt[]{\frac{a^{2} + b^{2} + c^{2}}{3}} \end{matrix}

(4)

egyenlőtlenséggel.
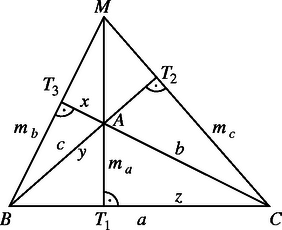
Ha a háromszög tompaszögű, akkor könnyen megtalálható hasonló háromszögpárok alapján (lásd 2. ábra)

\begin{matrix} A M : x = b : m_{a}, B M : y = c : m_{b}, C M : z = a : m_{c}, \end{matrix}

(5)

ahol

x = A T_{3}

és

y = B T_{2}

más szerepű szakaszok, mint az első részben. Az

m_{b}^{2}

kétféle kiszámítása révén

c^{2} - x^{2} = a^{2} - {(b + x)}^{2}

, amiből

x = \frac{a^{2} - b^{2} - c^{2}}{2 b}

. Hasonlóan kapjuk, hogy

y = \frac{a^{2} + c^{2} - b^{2}}{2 c}

és

z = \frac{a^{2} + b^{2} - c^{2}}{2 a}

. (5) alapján,

x

y

és

z

kifejezéseivel

\begin{matrix} \begin{matrix} m_{a} \cdot A M + m_{b} \cdot B M + m_{c} \cdot C M = b \cdot x + c \cdot y + a \cdot z = \\ = \frac{a^{2} - b^{2} - c^{2}}{2} + \frac{a^{2} + c^{2} - b^{2}}{2} + \frac{a^{2} + b^{2} - c^{2}}{2} = \\ = \frac{3 a^{2} - b^{2} - c^{2}}{2} = \frac{a^{2} + (a^{2} - c^{2}) + (a^{2} - b^{2})}{2} > \frac{a^{2} + b^{2} + c^{2}}{2}, \end{matrix} \end{matrix}

ahol felhasználtuk, hogy az

a

oldallal szemben van a tompaszög, és ezért

a^{2} > b^{2} + c^{2}

. Így most is a (3) egyenlőtlenséget kell igazolnunk.
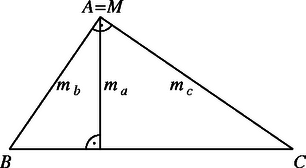
Ha a háromszög derékszögű (3. ábra), akkor

\begin{matrix} m_{a}^{2} + m_{b}^{2} + m_{c}^{2} = m_{a}^{2} + A B^{2} + A C^{2}, \end{matrix}

tehát azt kell bebizonyítanunk, hogy

\begin{matrix} m_{a}^{2} + A B^{2} + A C^{2} \leq \frac{3}{2} (A B^{2} + A C^{2}), \end{matrix}

azaz

\begin{matrix} m_{a}^{2} \leq \frac{1}{2} (A B^{2} + A C^{2}) = \frac{1}{2} B C^{2}, \end{matrix}

ami nyilvánvaló, sőt

m_{a}^{2} \leq \frac{1}{4} B C^{2} < \frac{1}{2} B C^{2}

.
Világos, hogy egyenlőség csak hegyesszögű háromszög esetén lehetséges. Az F. 2972. feladat I. megoldásából és (4)-ből látjuk, hogy az egyenlőség akkor és csak akkor áll fenn, ha

a = b = c

Gerő Tamás Miklós (Fazekas M. Főv. Gyak. Gimn., III. o.t.) dolgozata alapján

Megjegyzések. 1. Érdemes megemlíteni, hogy a feladat kitűzője az F. 2972. megoldása közben talált rá erre az összefüggésre.
2. A feladat állításánál valamivel többet bizonyítottunk, éspedig:

\begin{matrix} m_{a}^{2} + m_{b}^{2} + m_{c}^{2} \leq {(\frac{a + b + c}{2})}^{2} \leq \frac{3}{4} (a^{2} + b^{2} + c^{2}) \leq \frac{3}{2} (m_{a} \cdot A M + m_{b} \cdot B M + m_{c} \cdot C M) . \end{matrix}

3. Több megoldónk olyan összefüggéseket használt, amelyek bármilyen háromszög esetén érvényesek, és így nem kellett eseteket megkülönböztetniök.