Kezdőlap


Feladat:	N.28	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csörnyei Marianna , Futó Gábor , Szeidl Ádám
Füzet:	1995/február, 98 - 100. oldal		PDF \| MathML
Témakör(ök):	Sokszög lefedések, Terület, felszín, Paralelogrammák, Szabályos sokszögek geometriája, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1994/március: N.28

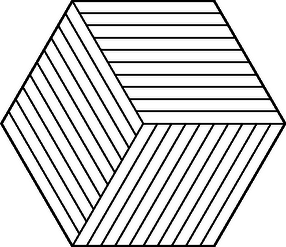
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy egy szabályos hatszög pontosan akkor bontható fel $n$ egyenlő területű paralelogrammára, ha $n$ osztható 3-mal.
A feltétel elégséges. Ha ui. $n$ $3$ -mal osztható, akkor egy szabályos hatszög a középpontjából a másodszomszédos csúcsaihoz húzott szakaszokkal 3 olyan egybevágó paralelogrammára bomlik, amelyek mindegyike tovább osztható $n / 3$ ‐ $n / 3$ darab egybevágó paralelogrammára, és ezzel végül is a hatszög $n$ darab egybevágó (és ezért egyenlő területű) paralelogrammára bomlik.

1. ábra

2. ábra

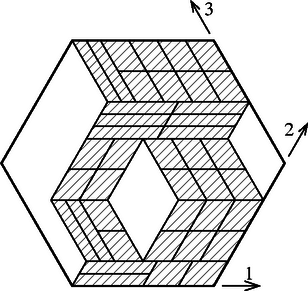
Megmutatjuk, hogy a feltétel szükséges is. Tegyük fel először, hogy a szabályos hatszöget tetszőlegesen osztottuk fel véges sok paralelogrammára. Tekintsük a felosztás valamelyik

P

paralelogrammájának egy

a

oldalát. A

P

-hez az

a

-ban néhány másik paralelogramma kapcsolódik, ezeknek

a

-val párhuzamos oldalaihoz pedig újabbak és újabbak, és ezt a sort folytathatjuk egészen addig, amíg el nem jutunk a hatszög valamelyik oldalához. Mivel a számba vett paralelogrammák sorra az

a

-val párhuzamos oldalaikban kapcsolódtak egymáshoz, azért a sor végét jelentő hatszögoldalnak is párhuzamosnak kell lennie

a

-val. Így beláttuk, hogy a felosztásban szereplő paralelogrammák mindegyik oldala párhuzamos valamelyik hatszögoldallal. A hatszög oldalai 3 irányt határoznak meg, ezeket a továbbiakban 1-, 2-, ill. 3-iránynak nevezzük. Tekintsük a hatszög valamelyik 1-irányú oldalát, és színezzük ki az ehhez kapcsolódó paralelogrammákat. A kiszínezett paralelogrammákhoz 1-irányú oldalaikon keresztül újabb és újabb paralelogrammák kapcsolódnak, amelyeket ugyancsak színezzünk ki. Ezt az eljárást ismételjük mindaddig, amíg el nem érjük a hatszög másik 1-irányú oldalát. A kiszínezett paralelogrammák ekkor egy

S_{1}

sávot alkotnak. Hasonlóan kapjuk az

S_{2}

, ill.

S_{3}

sávot, amelyek végein a hatszög 2-, ill. 3-irányú oldalai vannak. A továbbiakban nevezzünk egy paralelogrammát

i j

-paralelogrammának, ha annak oldalai az

i

- és a

j

-irányt határozzák meg; az

i j

-paralelogrammák összterülete legyen

t_{i j}

. Láttuk, hogy a felbontásban minden paralelogramma 12-, 23- vagy 31-paraleolgramma, tehát pl. az

S_{1}

sáv területe

t_{12} + t_{31}

. Messük most el az

S_{1}

-et tetszőleges 1-irányú egyenessel. Ekkor az egyenesnek a sávba eső szakaszai egy, a hatszög oldalával megegyező hosszúságú szakaszt alkotnak, ui. a szakaszokat a sávbeli paralelogrammákon keresztül a hatszög bármelyik 1-irányú oldalába eltolhatjuk úgy, hogy az eltolt példányok egymáshoz a végpontokban kapcsolódva ezt az oldalt adják ki. Ha most az

S_{1}

-et a benne szereplő paralelogrammák 1-irányú oldalegyeneseivel felszeleteljük kisebb sávokra, akkor előző megállapításunk értelmében a kisebb sávok összterülete megegyezik a hatszög két 1-irányú oldala által kifeszített paralelogrammának a területével. Hasonló mondható el az

S_{2}

és az

S_{3}

sávról is, mindebből pedig az következik, hogy

S_{1}

S_{2}

és

S_{3}

területe megegyezik:

\begin{matrix} t_{12} + t_{31} = t_{23} + t_{12} = t_{31} + t_{23}, \end{matrix}

azaz

\begin{matrix} t_{12} = t_{23} = t_{31} . \end{matrix}

Most már igen egyszerűen megkapjuk a megoldás elején megfogalmazott feltétel szükségességét, ha ui. a hatszöget

n

darab egyenlő területű paralelogrammára bontjuk fel, akkor az utóbbi egyenlőség azt jelenti, hogy az 12-, 23-, ill. 31-paralelogrammák száma egyenlő, vagyis

n

(3 egyenlő szám összegeként) 3-mal osztható.

Megjegyzések. 1. Csörnyei Marianna (Fazekas M. Főv. Gyak. Gimn.) kiemelte azt a megoldásunkból is kiolvasható megállapítást, hogy bárhogyan is osztunk fel egy szabályos hatszöget (véges sok) paralelogrammára, azokból kiválasztható néhány, amelyek összterülete harmada a hatszög területének.
2. A megoldásban használt módszerrel az is megmutatható, hogy ha egy konvex sokszög felbontható véges sok paralelogrammára, akkor a sokszög szükségszerűen középpontosan szimmetrikus is, hiszen oldalai páronként párhuzamosak és egyenlő hosszúak.