Feladat: F.3020 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bánn Richárd ,  Bárász Mihály ,  Burcsi Péter ,  Ehreth Imre ,  Erdélyi László ,  Farkas Illés ,  Fey Dániel ,  Gergely Levente ,  Gyarmati Katalin ,  György András ,  Hegedűs Viktor ,  Herényi Gergely ,  Hertz István ,  Horváth István ,  Izsák Ferenc ,  Kasza Tamás ,  Koblinger Egmont ,  Kovács Baldvin ,  Makai Márton ,  Maróti Attila ,  Maróti Gábor ,  Nagy Katalin ,  Németh Ákos ,  Németh Zoltán ,  Puskás Zsolt ,  Raisz Dávid ,  Séllei Béla ,  Szádeczky-Kardoss Szabolcs ,  Szeredi Tibor ,  Terpai Tamás ,  Tóth Mariann ,  Valkó Benedek 
Füzet: 1995/február, 95 - 96. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Terület, felszín, Négyzetrács geometriája, Feladat
Hivatkozás(ok):Feladatok: 1994/május: F.3020

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Néhány megoldónk a feladat szövegében az első mondat rövid, konvencionális megfogalmazását nem tartotta pontosnak. Ezért most a megoldásban tisztázzuk, hogy az A, B, C, D pontok ‐ a leírt sorrendben ‐ egy 10×10-es rácsnégyzet (különböző) csúcsai, és e négyzet oldalai a rács főegyeneseivel (a hálózatot alkotó egyenesekkel) párhuzamosak.

 
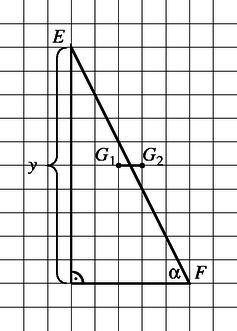
1. ábra
 

Abból, hogy melyik bábuval melyik csúcsba kell eljutnunk, megállapítható, hogy a bábuk alkotta háromszög körüljárásának iránya a lépéssorozat végére megváltozott. Ez azt jelenti, hogy valamelyik bábu valamelyik lépésével átmetszette a másik két bábut összekötő egyenest. Legyen e két bábu E és F, az pedig, amellyel átléptük az EF egyenest, G. Legyen G-nek az átlépés előtti helyzete G1, az átlépés utáni G2. Mivel a G1G2 távolság 1 egység, a G pontnak az EF egyenestől mért legkisebb távolságára, legyen ez m,  m≤0,5⋅sinα, ahol α az EF és G1G2 egyenesek hajlásszöge. Az 1. ábra jelöléseivel sinα=yEF, és így az EFG háromszög t területe:
t=EF⋅m2≤EF⋅0,5⋅yEF2=y4.
Mivel az E, F, G pontok egy 10×10-es négyzetlemezen vannak, y≤10, és így t≤2,5.
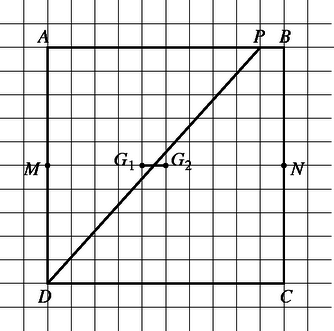
Megmutatjuk, hogy a t=2,5 lehetséges. A 2. ábrán az A ponton álló bábut az M és N pontokon keresztül vittük B-be, a B-n állót a P ponton keresztül A-ba, és a C-n állú bábut a legrövidebb úton D-be. Eközben a PG1D és PG2D háromszögek területe 2,5 volt, a bábuk alkotta többi háromszög területe pedig 2,5-nél több.

2. ábra

 
3. ábra

 

 Gergely Levente (Debrecen, Fazekas M. Gimn., IV. o.t.)

 
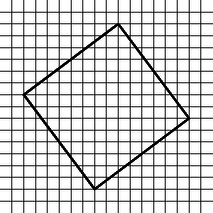
Megjegyzés. A feladat eredeti szövege megengedte a 3. ábra szerinti 10×10-es négyzetet is. Az elmondott megoldáshoz hasonlóan azt találjuk, hogy ekkor t legnagyobb értéke 3.
 Burcsi Péter (Pápa, Türr István Gimn., II. o.t.)
 
 Koblinger Egmont (Fazekas M. Főv. Gyak. Gimn., III. o.t.)