Kezdőlap


Feladat:	F.3093	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Braun Gábor , Frenkel Péter , Gyurkó L. Gergely , Lippner Gábor , Makai Márton , Mátrai Tamás , Szabó Jácint , Szente Márk Zsombor , Terpai Tamás , Vörös Zoltán
Füzet:	1997/március, 159 - 162. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Feladat
Hivatkozás(ok):	Feladatok: 1995/november: F.3093

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A leképzés nyilván injektív (kölcsönösen egyértelmű) hiszen ha két különböző pont képe ugyanaz a pont lenne, akkor egy, e két pontot csúcsként tartalmazó téglalap négy csúcsának képe nem lehetne egy téglalap négy csúcsa. Jelöljük a feladatbeli leképzést a továbbiakban $φ$ -vel. Állításunkat a következő lépéseken keresztül látjuk be.
(1) A $φ$ leképzés derékszögű háromszöget tart, azaz bármely derékszögű háromszög három csúcsának képe egy derékszögű háromszög három csúcsa. Legyenek ugyanis $A$ , $B$ , $C$ egy derékszögű háromszög csúcsai. Egészítsük ki a háromszöget egy $A B C D$ téglalappá, ekkor $φ (A)$ , $φ (B)$ , $φ (C)$ , $φ (D)$ egy téglalap csúcsai, így közülük bármelyik három egy derékszögű háromszög három csúcsa.
(2) A $φ$ megtartja a kollinearitást, pontosabban: ha az $x$ , $y$ , $z$ pontok egy egyenesen fekszenek, akkor $φ (x)$ , $φ (y)$ , $φ (z)$ is egy egyenesen van.
A) Tegyük fel először, hogy az $A$ , $B$ , $C$ pontok nem kollineárisak. Ekkor csak véges sok olyan $P$ pont van, amelyre az $A B P$ , $A C P$ , $B C P$ háromszögek közül legalább kettő derékszögű. Ha ugyanis az $A B P$ háromszög derékszögű, akkor $P$ vagy az $A B$ mint átmérő ,,fölé'' rajzolt Thalész-körön van, vagy az $A B$ szakaszra annak valamelyik végpontjában emelt merőlegesen; hasonló igaz az $A C P$ és $B C P$ háromszögre is. A három Thalész kör nyilván különböző, és ‐ az $A$ , $B$ , $C$ -re tett feltevés miatt ‐ ugyanez igaz a hat egyenesre is. A két kör és hat egyenes közül ezért bármely kettőnek csak véges sok közös pontja lehet.
B) Ha $A$ , $B$ , $C$ egy egyenesen vannak, akkor végtelen sok olyan $P$ pont létezik, amelyre az $A B P$ , $A C P$ , $B C P$ háromszögek közül legalább kettő derékszögű; ilyen például a három pont közös egyenesére $A$ -ban, $B$ -ben vagy $C$ -ben emelt merőleges bármely pontja.
Tegyük fel ezután, hogy $X$ , $Y$ , $Z$ kollineáris ponthármas. B) szerint végtelen sok olyan $P$ pont van, amelyre az $X Y P$ , $X Z P$ , $Y Z P$ háromszögek közül legalább kettő derékszögű, és minden ilyen $P$ -re $φ (P)$ is ilyen tulajdonságú pont lesz $φ (X)$ , $φ (Y)$ , $φ (Z)$ -hez (1) miatt. Végtelen sok ilyen $φ (P)$ van, hiszen $φ$ injektív; ezért A) miatt a $φ (X)$ , $φ (Y)$ , $φ (Z)$ hármas is kollineáris.
(3) $φ$ megtartja az egy egyenesen lévő pontok rendezését.
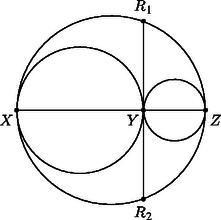
A) Ha $X$ , $Y$ , $Z$ különbözők és egy egyenesen vannak, akkor pontosan két olyan $R$ pont van, amelyre az $X Y R$ , $X Z R$ , $Y Z R$ háromszögek mindegyike derékszögű. Ha például $Y$ az $X$ és $Z$ között helyezkedik el, akkor $R$ csak az $X Z$ szakasz Thalész-körének és az $X Z$ -re $Y$ -ban állított merőlegesnek a (két) metszéspontja lehet. (A másik két Thalész-kör nem metszi a harmadik pontban állított merőlegest lásd. 1. ábra.) Megállapíthatjuk, hogy az $R_{1} X R_{2}$ , $R_{1} Y R_{2}$ , $R_{1} Z R_{2}$ hármasok közül egyedül $R_{1} Y R_{2}$ kollineáris.
B) Tegyük fel, hogy a páronként különböző $A$ , $B$ , $C$ pontok egy egyenesen fekszenek, és $B$ az $A$ és $C$ között helyezkedik el. Tekintsük azokat ‐ az A) szerint kizárólagosan létező ‐ $P_{1}$ és $P_{2}$ pontokat, amelyekre $A B P_{1}$ , $A C P_{1}$ , $B C P_{1}$ , $A B P_{2}$ , $A C P_{2}$ , $B C P_{2}$ mindegyike derékszögű. Mivel $φ$ kölcsönösen egyértelmű, azért $φ (A)$ , $φ (B)$ , $φ (C)$ is különbözőek, és (2) miatt kollineárisak. Az (1) szerint $φ (P_{1})$ és $φ (P_{2})$ az a két (különböző) pont, amely $φ (A)$ , $φ (B)$ , $φ (C)$ közül bármelyik kettővel derékszögű háromszöget határoz meg. Az A) szerint így a $φ (P_{1}) φ (A) φ (P_{2})$ , $φ (P_{1}) φ (B) φ (P_{2})$ , $φ (P_{1}) φ (C) φ (P_{2})$ ponthármasok közül egyedül az kollineáris, amelyik $φ (A)$ , $φ (B)$ , $φ (C)$ közül a közbülső helyzetű pontot tartalmazza. Azonban feltevésünkből következik, hogy a $P_{1}$ , $B$ , $P_{2}$ pontok egy egyenesen vannak, ezért (2) szerint a $φ (P_{1})$ , $φ (B)$ , $φ (P_{2})$ pontok is egy egyenesen fekszenek. Az A)-beli megállapítás értelmében ez csak úgy lehet, hogy $φ (B)$ a $φ (A)$ és $φ (C)$ között helyezkedik el.

(4)

φ

felezőpontot tart, azaz, ha

Y

R_{1} R_{2}

szakasz felezőpontja, akkor a

φ (R_{1}) φ (R_{2})

szakasz felezőpontja

φ (Y)

.
Tegyük fel, hogy az

R_{1} R_{2}

szakasz felezőpontja

Y

. Ekkor található két olyan (egymástól és

Y

-tól különböző)

X

és

Z

pont, amelyek által meghatározott szakasznak az

Y

belső pontja, és amelyre az

R_{j} X Y

R_{j} X Z

R_{j} Y Z

háromszögek mindegyike derékszögű. A (3) miatt ekkor

φ (Y)

φ (X) φ (Z)

szakasz belső pontja, és (1) szerint a

φ (R_{j}) φ (X) φ (Y)

φ (R_{j}) φ (X) φ (Z)

φ (R_{j}) φ (Y) φ (Z)

háromszögek mindegyike derékszögű. A 3A)-ban láttuk, hogy ekkor

φ (R_{1})

és

φ (R_{2})

nem más, mint a

φ (X) φ (Z)

szakasz Thalész-körének a

φ (X) φ (Z)

-re

φ (Y)

-ban állított merőlegessel való két metszéspontja. A két metszéspont a kör

φ (X) φ (Z)

átmérőjére szimmetrikus helyzetű lévén

φ (X)

felezi a

φ (R_{1}) φ (R_{2})

szakaszt. A bizonyított (4) tulajdonság következménye, hogy ha egy szakaszt

n

egyenlő részre osztunk, akkor az osztópontok képei a végpontok képei által meghatározott szakaszt

n

egyenlő részre osztják.

(5) Ha

A

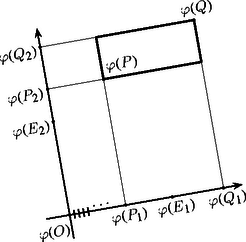
B

C

D

egy négyzet négy csúcsa, amelyek ebben a sorrendben követik egymást, és a négyzet középpontja

K

, akkor

φ (A)

φ (B)

φ (C)

φ (D)

is egy négyzet négy egymást ebben a sorrendben követő csúcsa, és a

φ (A) φ (B) φ (C) φ (D)

négyzet középpontja

φ (K)

.
A

φ (A)

φ (B)

φ (C)

φ (D)

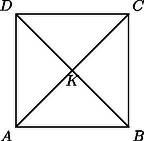
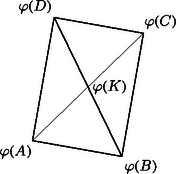
pontok szükségképpen egy téglalap csúcsai (2. ábra). Az

A C

és

B D

szakaszok közös felezőpontja

K

, ezért

φ

kölcsönös egyértelműsége és (4) miatt

φ (K)

φ (A) φ (C)

és

φ (B) φ (D)

szakaszok közös felezőpontjaként a téglalap középpontja, mivel

φ (A) φ (C)

és

φ (B) φ (D)

csak átlók lehetnek. Mivel

A K B

derékszögű háromszög, azért

φ (A) φ (K) φ (B)

is derékszögű háromszög (1) miatt.
Így a

φ (A) φ (B) φ (C) φ (D)

téglalap négyzet.
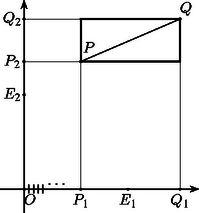
(6) Vegyünk fel a síkon egy

O

kezdőpontú derékszögű koordinátarendszert, a koordinátatengelyek

E_{1}

E_{2}

pontjaira legyen

\bar{O E_{1}} = \bar{O E_{2}} = 1

(3. ábra). A

φ (E_{1}) φ (O) φ (E_{2})

háromszög egyenlőszárú derékszögű (5) miatt; legyen

\bar{φ (O) φ (E_{1})} = \bar{φ (O) φ (E_{2})} = e

, és tekintsük a

φ (E_{1})

φ (E_{2})

φ (O)

pontok által meghatározott koordinátarendszert. Legyen

P Q

egy tetszőleges szakasz, a

P

és

Q

pontok merőleges vetületeit a koordinátatengelyekre jelölje

P_{1}

Q_{1}

P_{2}

Q_{2}

. Az (5) bizonyításából látható, hogy minden téglalap egymást követő csúcsainak

φ

-nél vett képei a megfelelő téglalap egymást követő csúcsai,

φ

-től függően vagy mindig az eredetivel azonos, vagy mindig azzal ellentétes körüljárásban. Ezért a

φ (P)

φ (Q)

pontok merőleges vetületei az ,,új'' koordinátarendszer tengelyeire

φ (P_{1})

φ (P_{2})

φ (Q_{1})

φ (Q_{2})

.
Legyen

n

tetszőleges pozitív egész szám, és mérjük fel az

O P_{1}

szakaszra

O

-tól kezdve az egységszakasz

(\bar{O E_{1}})

\frac{1}{n}

-szeresét a lehető legtöbbször; tegyük fel, hogy ezt

k

-szor tudtuk megtenni, így

\frac{k}{n} \leq \bar{O P_{1}} < \frac{k + 1}{n}

. Ekkor (4) miatt az

e

hosszúságú

φ (O) φ (E_{1})

szakasz

\frac{1}{n}

-szeresét is

k

-szor tudjuk rámérni a

φ (O) φ (P_{1})

szakaszra (felhasználva (4)-nek azt a következményét is, hogy ha egy

A B

szakasz

P

pontjára

\bar{A P} < \bar{P B}

teljesül, akkor a

P B

szakasz

\bar{A P} = \bar{P A_{1}}

egyenlőséget kielégítő

A_{1}

pontjával

\bar{φ (A) φ (P)} = \bar{φ (P) φ (A_{1})} < \bar{φ (P) φ (A_{1})} + \bar{φ (A_{1}) φ (B)} = \bar{φ (P) φ (B)}

). Ezért

\begin{matrix} \begin{matrix} k \frac{e}{n} \leq \bar{φ (O) φ (P_{1})} < (k + 1) \frac{e}{n}, \\ tehát \\ | \bar{O P_{1}} - \frac{1}{e} \bar{φ (O) φ (P_{1})} | < \frac{1}{n} . \end{matrix} \end{matrix}

Mivel ez minden

n

pozitív egészre elmondható,

\bar{φ (O) φ (P_{1})} = e \cdot \bar{O P_{1}}

adódik, akárcsak

\bar{φ (O) φ (P_{2})} = e \cdot \bar{O P_{2}}

\bar{φ (O) φ (Q_{1})} = e \cdot \bar{O Q_{1}}

\bar{φ (O) φ (Q_{2})} = e \cdot \bar{O Q_{2}}

. Tehát

\begin{matrix} \begin{matrix} \bar{φ (P) φ (Q)} & = \sqrt[]{{\bar{φ (P_{1}) φ (Q_{1})}}^{2} + {\bar{φ (P_{2}) φ (Q_{2})}}^{2}} = \\ = \sqrt[]{{(\bar{φ (O) φ (Q_{1})} - \bar{φ (O) φ (P_{1})})}^{2} + {(\bar{φ (O) φ (Q_{2})} - \bar{φ (O) φ (P_{2})})}^{2}} = \\ = \sqrt[]{{[e (\bar{O Q_{1}} - \bar{O P_{1}})]}^{2} + {[e (\bar{O Q_{2}} - \bar{O P_{2}})]}^{2}} = e \bar{P Q}, \end{matrix} \end{matrix}

P

és

Q

pontok választásától függetlenül.
Ezzel beláttuk, hogy a síktranszformáció (1)‐(5) pontokban leírt tulajdonságaiból következik, hogy az egyben hasonlósági transzformáció is.