Kezdőlap


Feladat:	3029. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boja Bence , Borsos Júlia , Kacsuk Zsófia , Kormos Márton , Kránicz Ákos , Négyesi Gábor , Páles Csaba , Várkonyi Péter , Varró Gergely
Füzet:	1997/december, 563. oldal		PDF \| MathML
Témakör(ök):	Egyéb gördülés (Gördülés), Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1996/december: 3029. fizika feladat

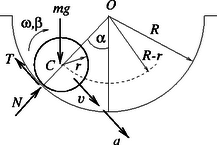
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a henger tömegközéppontjának valamely $α$ szöggel jellemzett helyhez tartozó pillanatnyi sebességét $v$ -vel, pályamenti gyorsulását $a$ -val, szöggyorsulását $β$ -val, a vájat által kifejtett nyomóerőt $N$ -nel, a tapadó súrlódási erőt pedig $T$ -vel (1. ábra).

A henger mozgásegyenlete a pályaérintő irányában

\begin{matrix} m g sin α - T = m a, \end{matrix}

(1)

sugárirányban

\begin{matrix} N - m g cos α = m \frac{v^{2}}{R - r}, \end{matrix}

(2)

a forgómozgás egyenlete pedig

\begin{matrix} T r = \frac{1}{2} m r^{2} β . \end{matrix}

(3)

A tiszta (csúszásmentes) gördülés feltétele szerint a hengernek a vájattal éppen érintkező pontja áll:

v - r ω = 0,

ahonnan

\begin{matrix} v = r ω, azaz a = r β . \end{matrix}

(4)

Felírhatjuk még a mechanikai energia megmaradását kifejező egyenletet:

\begin{matrix} m g (R - r) \cdot (cos α - cos α_{0}) = \frac{1}{2} m v^{2} + \frac{1}{2} (\frac{1}{2} m r^{2}) ω^{2}, \end{matrix}

(5)

ahol

α_{0} = 60^{\circ}

, tehát

cos α_{0} = \frac{1}{2}

Az (1) ‐ (5) egyenletrendszert megoldva az erőkre

\begin{matrix} T = \frac{m g}{3} sin α, \end{matrix}

(6)

\begin{matrix} N = \frac{m g}{3} (7 cos α - 2) \end{matrix}

(7)

adódik. (Érdekes, hogy a hengerre ható erők nem függnek sem a vájat, sem a henger sugarától, de még azok arányától sem.)
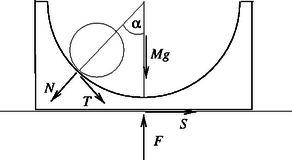
A vájat mozgásegyenletei a 2. ábra jelöléseivel:

\begin{matrix} F - M g - N cos α - T sin α = 0, \end{matrix}

(8)

\begin{matrix} S - N sin α + T cos α = 0, \end{matrix}

(9)

a meg nem csúszás feltétele pedig

\begin{matrix} μ_{0} F \geq S . \end{matrix}

(10)

A (6) és (7) kifejezéseket (8)-ba és (9)-be helyettesítve, majd azokból

S

-et és

F

-et kifejezve a (10) egyenlőtlenséget

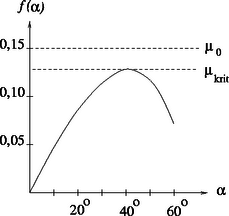
\begin{matrix} μ_{0} \geq 2 sin α \frac{3 cos α - 1}{6 cos^{2} α - 2 cos α + 11} \equiv f (α) \end{matrix}

(11)

alakra hozhatjuk. Ha ábrázoljuk az

f (α)

függvényt a

0 \geq α \geq 60^{\circ}

intervallumon (3. ábra), a grafikonról leolvashatjuk, hogy

f (α) \leq μ_{krit} \approx 0, 13

. A megadott számadatokkal a

(11)

feltétel minden szögnél teljesül, a henger tehát egyáltalán nem csúszik meg.

Borsos Júlia (Győr, Révai M. Gimn., III. o.t.)