Feladat:	3005. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gönci Balázs ,  Kurucz Keve ,  Németh Péter
Füzet:	1997/március, 183. oldal		PDF  |  MathML
Témakör(ök):	Egyéb párhuzamos erők eredője, Tömegközéppont helye, Feladat
Hivatkozás(ok):	Feladatok: 1996/október: 3005. fizika feladat

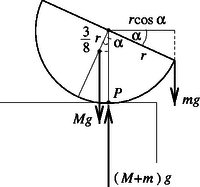
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a félgömb tömegét $M$-mel, a sugarát $r$-rel, a nehezék tömegét pedig $m$-mel. Egyensúlyi helyzetben a testre ható erők eredő forgatónyomatéka bármely pontra nézve nulla kell legyen. Írjuk fel például az 1. ábrán látható $P$ pontra vonatkoztatva a nyomatékok egyensúlyát: $\begin{array}{c}{\displaystyle Mg\frac{3r}{8}\text{sin}\alpha =mgr\text{cos}\alpha \mathrm{,}}\end{array}$ ahonnan a $M=2m$ felhasználásával $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =4/\mathrm{3,}$ azaz $\alpha =53\mathrm{,}{1}^{\circ }$ adódik.  Kurucz Keve (Révkomárom, Selye J. Gimn., I. 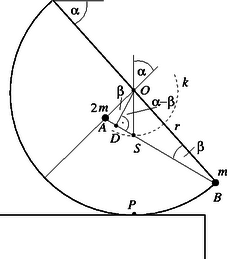o.t.)   II. megoldás. A félhengert helyettesíthetjük az $A$ tömegközéppontjába helyezett $2m$ tömegű pontszerű testtel (2. ábra), a nehezéket pedig a $B$ pontba helyezett $m$ tömegponttal. Ennek az összetett rendszernek az $AB$ szakaszt harmadoló $S$ pontban van a közös tömegközéppontja. Ha a félgömböt képzeletben elfordítjuk, az $S$ pont az $O$ középpontú $k$ körön mozdul el. Egyensúlyi helyzetben az $S$ pont a $k$ kör legmélyebb pontjában, vagyis az $O$ középpont alatt helyezkedik el. (Az $O$ pont az elforgatás során az asztallaptól mindvégig $r$ távolságban marad.) Az $ABO$ derékszögű háromszögből $\begin{array}{c}{\displaystyle \beta =\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(3/8\right)=20\mathrm{,}{56}^{\circ }\text{ és }AS=\frac{1}{3}AB=0\mathrm{,}3560r\mathrm{.}}\end{array}$ Az $AOD$ háromszögből $AD=\frac{3r}{8}\text{sin}\beta =0\mathrm{,}1317r\mathrm{,}$ $ODB$ háromszögből pedig $OD=\text{sin}\beta =0\mathrm{,}3511r$. Végül az $OSD$ háromszögből $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\alpha -\beta \right)=\frac{SD}{OD}=\frac{AS-AD}{OD}=\frac{0\mathrm{,}3560r-0\mathrm{,}1317r}{0\mathrm{,}3511r}=0\mathrm{,}\mathrm{6388,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle \alpha -\beta =32\mathrm{,}{57}^{\circ }\mathrm{,}\text{tehát}\alpha =\mathrm{32,}{57}^{\circ }+20\mathrm{,}{56}^{\circ }=53\mathrm{,}{13}^{\circ }\mathrm{.}}\end{array}$  Gönci Balázs (Budapest, Móricz Zs. Gimn., II. o.t.) és    Németh Péter (Jászapáti, Mészáros L. Gimn., II. o.t.) dolgozata alapján