Kezdőlap


Feladat:	2989. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fancsali Szabolcs , Hegyi Barnabás , Négyesi Gábor
Füzet:	1996/október, 445. oldal		PDF \| MathML
Témakör(ök):	Vastag lencse, Feladat
Hivatkozás(ok):	Feladatok: 1996/május: 2989. fizika feladat

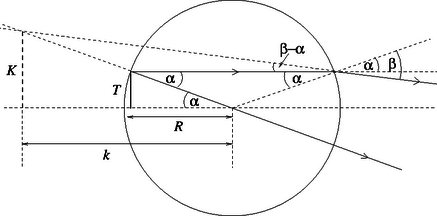
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az akvárium távolabbi szélénél úszó $T$ nagyságú halat a középponttól $k$ távolságban $K$ méretűnek látjuk. Az ábrán látható sugármenetek és a törési törvény felhasználásával (és valamennyi bejelölt szög kicsinysége miatt a szinuszokat és a tangenseket a szögekkel közelítve) kapjuk, hogy

\begin{matrix} \begin{matrix} \frac{K}{T} & = \frac{k}{R}, \\ K - T & = (k + R) (β - α), \\ \frac{β}{α} & = n, \\ \frac{T}{R} & = α . \end{matrix} \end{matrix}

(

n

a víz törésmutatója.) A fenti egyenletekből

\begin{matrix} k = \frac{n}{2 - n} R és K = \frac{n}{2 - n} T \end{matrix}

adódik.
Az akvárium közelebbi szélénél a halat

T

méretűnek látjuk. Az (abszolút) nagyítások aránya tehát (

n

-et

4 / 3

-nak véve)

\begin{matrix} N_{absz} = \frac{K_{távol}}{K_{közel}} = \frac{n}{2 - n} = \frac{4 / 3}{2 - 4 / 3} = 2. \end{matrix}

A hal látszólagos méretét nem a képének abszolút nagysága, hanem annak látószöge jellemzi. Ha a szemünk az akváriumtól a sugár

c

-szeresének megfelelő távolságban van, akkor a látószögek:

\begin{matrix} φ_{távol} = \frac{K}{k + R + c R}, illetve φ_{közel} = \frac{T}{c R} . \end{matrix}

A szögnagyítások aránya:

\begin{matrix} N_{szög} = \frac{φ_{távol}}{φ_{közel}} = \frac{K}{T} \cdot \frac{c}{(k / R) + c + 1} = \frac{n}{2 - n} \cdot \frac{c}{\frac{n}{2 - n} + c + 1} = \frac{n \cdot c}{n + (2 - n) (c + 1)} . \end{matrix}

n = 4 / 3

-dal számolva

\begin{matrix} N_{szög} = \frac{2 c}{3 + c}, \end{matrix}

ami a feladat számadataival (

c = 1

)

N_{szög} = 1 / 2

. A hal tehát kétszer kisebbnek látszik a távolabbi helyzetében, mint a közelebbiben. Ha nagyon messziről nézzük az aranyhalat (

c ≫ 1

), akkor éppen fordított az arány, a közelebbi helyzetben látszik kétszer kisebbnek, s ha

c = 3

, tehát a sugár háromszorosának megfelelő helyről nézve a szögnagyítások éppen egyformák.

Több megoldás alapján

Megjegyzés. A megoldás során feltételeztük, hogy a hal a gömb egyik főköre mentén úszik.