Feladat:	2940. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Jegenyés Nikoletta ,  Mátrai Tamás ,  Négyesi Gábor
Füzet:	1996/május, 313. oldal		PDF  |  MathML
Témakör(ök):	Pillanatnyi forgástengely, Forgási energia, Feladat
Hivatkozás(ok):	Feladatok: 1995/december: 2940. fizika feladat

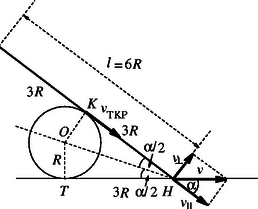
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A szalmaszál mozgási energiája a tömegközéppontba képzelt teljes tömeg haladó (transzlációs) mozgási energiájából és a tömegközéppont körüli forgás energiájából tevődik össze: $\begin{array}{c}{\displaystyle E=\frac{1}{2}m{v}_{\text{TKP}}^2+\frac{1}{2}{\Theta }_{\text{TKP}}{\omega }^2\mathrm{.}}\end{array}$ (1) A felezőpont sebessége a szóbanforgó pillanatban érintő irányú, nagysága pedig megegyezik a hangya sebességének szalmaszál irányú komponensével (1. ábra): $\begin{array}{c}{\displaystyle v_{\text{TKP}}=v_{\Vert }=v\text{cos}\alpha \mathrm{.}}\end{array}$ A hangya sebességének a szalmaszálra merőleges komponense a tömegközéppont körüli forgás kerületi sebessége, így ($R$-rel jelölve a faág sugarát) $\begin{array}{c}{\displaystyle v_{\perp }=3R\omega \mathrm{,}\text{ahonnan}\omega =\frac{v_{\perp }}{3R}=\frac{v\text{sin}\alpha }{3R}\mathrm{.}}\end{array}$ Hátravan még az $\alpha$ szög meghatározása. Az $OTH$ háromszögben látható, hogy $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{\alpha }{2}=\frac{R}{3R}=\frac{1}{3}\mathrm{,}}\end{array}$ ahonnan trigonometriai azonosságok felhasználásával $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{3}{5}\mathrm{,}\text{illetve}\text{cos}\alpha =\frac{4}{5}\mathrm{.}}\end{array}$ Mivel a szalmaszál tehetetlenségi nyomatéka $\begin{array}{c}{\displaystyle {\Theta }_{\text{TKP}}=\frac{1}{12}m{l}^2=3m{R}^2\mathrm{,}}\end{array}$ a fenti kifejezéseket (1)-be helyettesítve a keresett energiára $\begin{array}{c}{\displaystyle E=\frac{1}{2}m{v}^2\text{cos}{}^2\alpha +\frac{1}{2}3m{R}^2\cdot \frac{v^2\text{sin}{}^2\alpha }{9R^2}=\frac{19}{50}m{v}^2\mathrm{.}}\end{array}$  Jegenyés Nikoletta (Pécs, Széchenyi I. Gimn., III. o.t.) és    Négyesi Gábor (Eger, Szilágyi E. Gimn., III. 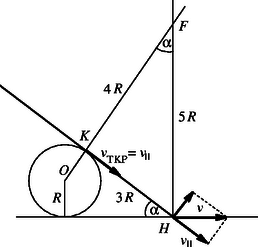o.t.) dolgozata alapján   II. megoldás. A szalmaszál transzlációs és forgó mozgása minden pillanatban helyettesíthető egy alkalmazan választott ,,pillanatnyi forgástengely'' körüli forgással. Bármely pont kerületi sebessége merőleges a forgástengelyt a ponttal összekötő egyenesre, a ,,sugárra''. A forgástengelynek a mozgás síkjába eső pontja tehát úgy kapható meg, hogy a szalmaszál két tetszőleges pontjában merőlegest állítunk a sebességre, és megkeressük ezen egyenesek metszéspontját. Legyen ez a két pont például a szalmaszál középpontja és az a végpont, ahol a hangya van (2. ábra). A $HFK\sphericalangle$ egyenlő az I. megoldásban $\alpha$-val jelölt $THK\sphericalangle$-gel, mert merőleges szárú hegyesszögek. $\alpha$-t ugyanúgy határozhatjuk meg, mint az I. megoldásban. A $\text{sin}\alpha =\frac{3}{5}$, $\text{cos}\alpha =\frac{4}{5}$, $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{3}{4}$ értékek felhasználásával a $HKF$ háromszögből $\begin{array}{c}{\displaystyle HF=\frac{3R}{\text{sin}\alpha }=5R\mathrm{,}\text{illetve}FK=\frac{3R}{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }=4R\mathrm{.}}\end{array}$ A $H$ pont kerületi sebessége $v$, tehát az $F$ pillanatnyi forgástengely körüli forgás szögsebessége $\begin{array}{c}{\displaystyle {\omega }_{\text{F}}=\frac{v}{5R}\mathrm{.}}\end{array}$ A Steiner-tétel szerint a szalmaszál tehetetlenségi nyomatéka $F$-re vonatkoztatva $\begin{array}{c}{\displaystyle {\Theta }_{\text{F}}={\Theta }_{\text{TKP}}+m{\left(4R\right)}^2=19m{R}^2\mathrm{,}}\end{array}$ a forgási energia pedig $\begin{array}{c}{\displaystyle E=\frac{1}{2}{\Theta }_{\text{F}}{\omega }_{\text{F}}^2=\frac{19}{50}m{v}^2\mathrm{.}}\end{array}$  Jegenyés Nikoletta (Pécs, Széchenyi I. Gimn., III. o.t.) és    Mátrai Tamás (Fazekas M. Főv. Gyak. Gimn., III. o.t.) dolgozata alapján   Megjegyzés. Ellenőrizhető, hogy a kétféle megoldásban különböző forgástengelyekre ugyanakkora szögsebesség adódott. Ez nem véletlen, hanem általánosan igaz: bármely merev test szögsebessége független a forgástengely megválasztásától.