Kezdőlap


Feladat:	2933. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Böde Csaba , Csekő Lehel , Kurucz Zoltán , Perényi Márton , Tóth Gábor Zsolt , Varró Gergely
Füzet:	1996/május, 310. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Merev test impulzusnyomatéka (perdülete), Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1995/november: 2933. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A pálca mozgása három szakaszra osztható. Az I. szakaszban még mindkét szöghöz hozzáér a pálca, mozgása ekkor forgás nélküli egyenesvonalú, de nem egyenletesen gyorsuló mozgás. Ha a súrlódás nem túl erős, akkor a pálca felső vége valamekkora $v_{0}$ sebességgel eléri a $B$ szöget és megkezdődik a mozgás II. szakasza. Ebben a szakaszban a pálcára a nehézségi erő és az $A$ szög által kifejtett erő (nyomóerő és súrlódási erő) hat, melyek hatására a test tömegközéppontja valamilyen síkgörbe mentén gyorsulva mozog, s emellett a pálca még a tömegközéppontja körül változó szöggyorsulású forgómozgást is végez. Ez a szakasz addig tart, míg a pálca felső vége el nem éri az $A$ szöget. Ezután, a III. szakaszban a pálcára már csak a nehézségi erő hat (ha a közegellenállást nem vesszük figyelembe), így a tömegközéppontja ferde hajításnak megfelelően kell mozogjon, a tömegközéppont körüli forgómozgás pedig egyenletes lesz.
A III. szakaszbeli (állandó) szögsebesség nagysága megegyezik a II. szakaszbeli mozgás végső szögsebességével, a feladat tehát ennek meghatározása.
Míg az I. és a III. szakasz mozgását leíró egyenleteket elemi úton, felsőbb matematikai módszerek alkalmazása nélkül meg tudjuk oldani, addig a II. szakaszbeli mozgás egyenletei nagyon bonyolultak (csatolt, nemlineáris differenciálegyenlet-rendszert alkotnak), pontos megoldásuk még felsőbb matematikai eszközökkel sem kapható meg. Ennek ellenére, a numerikus adatok ismeretében egy elég természetes fizikai feltevéssel élhetünk, amelynek jogosságát bizonyos pontossággal igazolni is tudjuk, s amely feltevés mellett a megoldás is végigvihető.
Ez a feltevés a következő: Feltételezzük, hogy az I. szakasz végére a pálca viszonylag nagy sebességre gyorsult fel, s ezzel (a későbbiekben még tovább növekvő) sebességgel olyan rövid $Δ t$ idő alatt csúszik végig az $A$ szögön, hogy közben nem tud számottevő mértékben elfordulni. A II. mozgásszakasz rövid ideje alatt a pálca sebességét és a vízszintessel bezárt szögét állandónak tekintjük, s ilyen feltételek mellett kiszámítjuk a szög által kifejtett $N$ nyomóerőt. Ennek az erőnek a forgatónyomatéka $Δ t$ idő alatt valamekkora perdületet ad a pálcának, s ez a perdület a III. szakaszban már változatlan marad.
Kövessük most végig a fentieket számolással is! Az előző, FF. 2932. feladat megoldása szerint az I. szakaszban a pálcára ható súrlódási erők összege ( $α = 45^{\circ}$ esetén):

\begin{matrix} S (x) = μ (N_{A} + N_{B}) = \frac{μ m g}{\sqrt[]{2}} (1 + \frac{2 x}{d}) . \end{matrix}

Látható, hogy

S (x)

x

-szel arányosan (lineárisan) változik, kezdetben

S (x = 0) = μ m g / \sqrt[]{2}

, a mozgásszakasz végén pedig (amikor

x = l / 2 - d = 4 d

) a súrlódási erők összege

S (4 d) = 9 μ m g / \sqrt[]{2}

. Az átlagos súrlódási erő ezek szerint

S_{átlag} = 5 μ m g / \sqrt[]{2}

.
A munkatétel segítségével kiszámíthatjuk, hogy mekkora

v_{0}

végsebességgel mozog a pálca az I. szakasz végén (és ami ezzel megegyező, a II. mozgásszakasz elején):

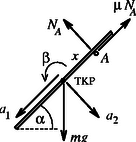
\begin{matrix} \begin{matrix} \frac{1}{2} m v_{0}^{2} + S_{átlag} \cdot 4 d = m g \cdot \frac{4 d}{\sqrt[]{2}}, \\ ahonnan v_{0} = \sqrt[]{4 \sqrt[]{2} \cdot g d (1 - 5 μ)} = \sqrt[]{4 \cdot 1,41 \cdot 9,81 \cdot 0,1 (1 - 5 \cdot 0,1)} \approx 1,66 m/s . \end{matrix} \end{matrix}

A II. mozgásszakaszban a pálca az ábrán látható erők hatására mozog. Kezdetben

α = 45^{\circ}

v = v_{0}

és

x = 4 d = 0,4 m

. A pálca megpördülése szempontjából az a lényeges, hogy mekkora az

N

erő (átlagos) forgatónyomatékának és a mozgás

Δ t

idejének szorzata. A pálca sebességének változását elhanyagolva a lecsúszás idejére

\begin{matrix} Δ t \approx \frac{d}{v_{0}} = \frac{0,1 m}{1,66 m/s} = 0,06 s \end{matrix}

adódik. A nyomóerőt a kezdeti pillanatban a pálcára merőleges irányú mozgásegyenletből és a forgómozgás egyenletéből kaphatjuk meg. Az ábra jelöléseit használva

\begin{matrix} \begin{matrix} m g cos 45^{\circ} - N = m a_{2}, \\ N \cdot 4 d = \frac{1}{12} m l^{2} \cdot β, \end{matrix} \end{matrix}

a kényszerfeltétel, hogy a pálcának a szöggel érintkező pontja nem gyorsul a pálcára merőlegesen:

\begin{matrix} a_{2} - 4 d \cdot β = 0. \end{matrix}

Ezekből az egyenletekből

\begin{matrix} N = \frac{m g cos 45^{\circ}}{1 + 12 {(4 d)}^{2} / l^{2}} \approx 0,24 m g . \end{matrix}

(Megjegyezzük, hogy az I. szakasz végén, tehát amikor a pálca még éppen hozzáért a

B

szöghöz, az

A

szögnél ható nyomóerő

5 m g cos 45^{\circ} \approx 3,5 m g

volt. Amikor a pálca lecsúszik a

B

szögről, a másik szögnél ható erő ugrásszerűen megváltozik, értéke hirtelen jelentősen lecsökken.) Ha a fenti számolást megismételjük a II. mozgásszakasz végének megfelelő, vagyis az

x = 5 d

helyzetre,

N \approx 0,18 m g

adódik. A nyomóerő tehát átlagosan

N_{átlag} = 0,21 m g

-nek vehető, s ennek a közelítésnek kb.

15 %

a pontossága. Az

N_{átlag}

erő forgatónyomatéka az átlagos

4,5 d = 0,45 m

nagyságú erőkarral

N_{átlag} \cdot 4,5 d

, így a forgómozgás alapegyenlete szerint az egyenletesnek feltételezett

β

szöggyorsulásra a következő egyenlet írható fel:

\begin{matrix} N_{átlag} \cdot 4,5 d = \frac{1}{12} m l^{2} \cdot β, \end{matrix}

ahonnan a numerikus adatokkal

β \approx 11 s^{- 2}

adódik.
Ezzel a szöggyorsulással

Δ t

idő alatt a pálca

\begin{matrix} Δ α = \frac{β}{2} {(Δ t)}^{2} \approx 0,02 radián \approx 1^{\circ} \end{matrix}

szöggel fordul el az

α = 45^{\circ}

-os helyzethez képest. Ez a szögelfordulás valóban nem jelentős, ez a korábbi feltevésünk jogosságát igazolja.
A pálca a II. szakasz végén

ω = β Δ t \approx 0,7 s^{- 1}

szögsebességre, tehát másodpercenkénti

f = 0,1

-es fordulatszámra gyorsul fel, s ezt a fordulatszámot a továbbiakban meg is tartja. A számolás kb. 15 százalék pontossággal hihető el, ennyi az ,,elméleti érték relatív hibája''.

Tóth Gábor Zsolt (Budapest, Árpád Gimn., IV. o.t.) megoldása alapján