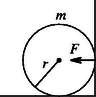
Vizsgáljuk a golyó mozgásának az asztal falára merőleges komponensét. A biliárdasztalon guruló golyó csúszásmentesen gördül. Ennek feltétele a $v=r\omega$ egyenlőség, ahol $v$ a tömegközéppont sebessége, $\omega$ pedig a szögsebesség. Ha a golyó rugalmasan ütközik az asztal falának, sebessége $-v$-re változik. Ha az asztal széle függőleges (1. ábra), akkor $\overrightarrow{F}$ hatásvonala átmegy a golyó tömegközéppontján. Így $\overrightarrow{F}$ forgatónyomatéka nulla, ezért a golyó szögsebessége nem változik, vagyis a visszapattanás után nem áll fenn a tiszta gördülés feltétele, a golyó csúszik. A csúszó súrlódás úgy változtatja meg a golyó sebességét és szögsebességét, hogy az ismét tisztán gördüljön. Eközben a sebessége jelentősen lecsökken.
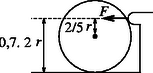
A tömegközéppont felett $h=\frac{2}{5}r$ távolságra ható erőnek forgatónyomatéka is van, így a szögsebességet is megváltoztatja (2. ábra). Ha az ütközés $\Delta t$ idő alatt zajlik le, akkor az impulzus, illetve az impulzusmomentum megváltozását leíró egyenletek: