Feladat:	2913. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bárász Mihály ,  Demkó László ,  Gubás Lóránt László ,  Lovász Mónika ,  Tóth Gábor Zsolt
Füzet:	1996/március, 186. oldal		PDF  |  MathML
Témakör(ök):	Gördülés vízszintes felületen, Feladat
Hivatkozás(ok):	Feladatok: 1995/szeptember: 2913. fizika feladat

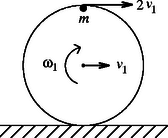
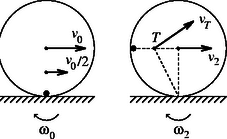
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. a) Jelöljük az abroncs középpontjának sebességét $v_1$-gyel abban a helyzetben, amikor a nehezék legfelül van. Az abroncs szögsebessége ekkor ${\omega }_1=v_1/R$, a nehezék sebessége pedig $2v_1$ (1. ábra). Az energiamegmaradás tétel szerint $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}_1^2+\frac{1}{2}m{R}^2{\left(\frac{v_1}{R}\right)}^2+\frac{1}{2}m{\left(2v_1\right)}^2+mg\left(2R\right)=\frac{1}{2}m{v}_0^2+\frac{1}{2}\left(m{R}^2\right){\left(\frac{v_0}{R}\right)}^2\mathrm{,}}\end{array}$ (1) ahonnan $\begin{array}{c}{\displaystyle v_1=\sqrt[]{\frac{v_0^2-2gR}{3}}\mathrm{.}}\end{array}$ (2) (Felhasználtuk, hogy az abroncs tehetetlenségi nyomatéka a középpontján átmenő tengelyre vonatkoztatva $\Theta =m{R}^2$, továbbá hogy egy merev test mozgási energiája a tömegközéppont mozgásának megfelelő $m{v}^2/2$ és a tömegközéppont körüli forgásnak megfelelő $\Theta {\omega }^2/2$ energiák összege.) 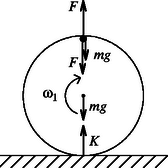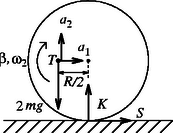A nehezék felső helyzetében a 2. ábrán látható erők hatnak az abroncsra, illetve a nehezékre. A nehezék függőleges irányú gyorsulása az ${\omega }_1$ szögsebességű forgásból származik: $a=R{\omega }_1^2=v_1^2/R$. A mozgásegyenletek: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle mg-K-F}& {\displaystyle =\mathrm{0,}}\hfill & \hfill {\displaystyle \left(3\right)}\\ \hfill {\displaystyle mg+F}& {\displaystyle =m\frac{v_1^2}{R}\mathrm{,}}\hfill & \hfill {\displaystyle \left(4\right)}\end{array}}}\end{array}$ amelyekből a talaj által kifejtett nyomóerő $\begin{array}{c}{\displaystyle K=2mg-\frac{m{v}_1^2}{R}\mathrm{.}}\end{array}$ (5) Az abroncs akkor nem emelkedik fel, ha $K\ge 0$, vagyis $v_1^2<2gR$. Ezt a feltételt (2)-vel összevetve a kezdősebességre a $\begin{array}{c}{\displaystyle v_0\le \sqrt[]{8gR}\approx 4\frac{\text{m}}{\text{s}}}\end{array}$ (6) megszorítás adódik. 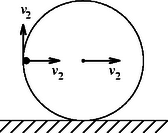b) Amikor a nehezék az abroncs középpontjával azonos magasságba kerül (például a 3. ábrán látható helyzetben), az energiatétel szerint az abroncs $v_2$ sebességére $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}_0^2+\frac{1}{2}\left(m{R}^2\right){\left(\frac{v_0}{R}\right)}^2=\frac{1}{2}m{v}_2^2+\frac{1}{2}\left(m{R}^2\right){\left(\frac{v_2}{R}\right)}^2+\frac{1}{2}m{\left(\sqrt[]{2}{v}_2\right)}^2+mgR\mathrm{,}}\end{array}$ (7) azaz $\begin{array}{c}{\displaystyle v_2=\sqrt[]{\frac{v_0^2-Rg}{2}}}\end{array}$ (8) adódik. 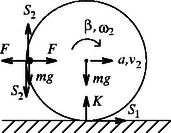(A nehezék teljes sebessége az abroncs vízszintes haladásából adódó $v_2$ és a forgásból származó függőleges irányú, ${\omega }_{2}R=v_2$ nagyságú sebességek vektori összege.) A mozgásegyenletek a 4. ábrán látható jelölésekkel a nehezékre $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle F}& {\displaystyle =m\left(a+\frac{v_2^2}{R}\right)\mathrm{,}}\hfill & \hfill {\displaystyle \left(9\right)}\\ \hfill {\displaystyle S_2-mg}& {\displaystyle =m\left(R\beta \right)\mathrm{,}}\hfill & \hfill {\displaystyle \left(10\right)}\\ \hfill {\displaystyle \text{az abroncsra pedig}{S}_1-F}& {\displaystyle =ma\mathrm{,}}\hfill & \hfill {\displaystyle \left(11\right)}\\ \hfill {\displaystyle mg+S_2-K}& {\displaystyle =\mathrm{0,}}\hfill & \hfill {\displaystyle \left(12\right)}\\ \hfill {\displaystyle S_{1}R+S_{2}R}& {\displaystyle =-\left(m{R}^2\right)\cdot \beta \mathrm{,}}\hfill & \hfill {\displaystyle \left(13\right)}\end{array}}}\end{array}$ ahol a csúszásmentes gördülés miatt az abroncs $\beta$ szöggyorsulása és tömegközéppontjának $a$ gyorsulása között fennáll: $\beta =a/R$. A (8)‐(13) egyenletrendszer megoldásából a keresett nyomóerő $\begin{array}{c}{\displaystyle K=\frac{1}{8}mg\left(15-\frac{v_0^2}{Rg}\right)\mathrm{.}}\end{array}$ (14) Ha a kezdősebesség éppen a (6) egyenlőtlenség határhelyzetének megfelelő, akkor $\begin{array}{c}{\displaystyle K=\frac{7}{8}mg\approx 14N\mathrm{.}}\end{array}$ (15) ugyanezt kapjuk a nehezék másik helyzetében, a leszálló ágban is.  Bárász Mihály (Fazekas M. Főv. Gyak. Gimn., IV. o.t.)   II. megoldás. b) Az abroncsot és a hozzá rögzített nehezéket tekintsük egyetlen merev testnek, amelynek tömege $2m$, a tömegközéppontja pedig az 5. ábrán látható $T$ pont. A $T$ pontra vonatkoztatva a rendszer tehetetlenségi nyomatéka (a Steiner-tétel felhasználásával) $\begin{array}{c}{\displaystyle {\Theta }_T={\Theta }_T^{\text{(abroncs)}}+{\Theta }_T^{\text{(nehezék)}}=m{R}^2+m{\left(\frac{R}{2}\right)}^2+m{\left(\frac{R}{2}\right)}^2=\frac{3}{2}m{R}^2\mathrm{.}}\end{array}$ (16) Ha a kezdeti $v_0$ sebességnek és ${\omega }_0=v_0/R$ szögsebességnek megfelelő energiát összehasonlítjuk a 6. ábrán látható helyzet $v_2$ sebességű és ${\omega }_2=v_2/R$ szögsebességű mozgáséval, az energia megmaradásának tétele szerint $\begin{array}{c}{\displaystyle \frac{2m}{2}{\left[\frac{v_0}{2}\right]}^2+\frac{1}{2}\left[\frac{3}{2}m{R}^2\right]\frac{v_0^2}{R}=\frac{2m}{2}\left[R^2+\frac{R^2}{4}\right]{\left[\frac{v_2}{R}\right]}^2+\frac{1}{2}\frac{3m{R}^2}{2}{\left[\frac{v_2}{R}\right]}^2+mgR\mathrm{,}}\end{array}$ (17) azaz $\begin{array}{c}{\displaystyle v_2=\sqrt[]{\frac{v_0^2-Rg}{2}}={\omega }_{2}R\mathrm{.}}\end{array}$ (18) (Mindkét helyzetben a mozgási energiát a tömegközéppont haladó mozgásából és a tömegközéppont körüli forgásból számoltuk. A szögsebességet a talajjal való érintkezési pont körüli forgásból határozhatjuk meg, de ugyanekkora szögsebességgel forog a rendszer a tömegközéppontja körül is.) A rendszer mozgását a 7. ábrán látható erőkkel és gyorsulásokkal az alábbi egyenlet írják le: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle K-2mg}& {\displaystyle =2m\cdot a_2\mathrm{,}}\hfill & \hfill {\displaystyle \left(19\right)}\\ \hfill {\displaystyle S}& {\displaystyle =2m\cdot a_1\mathrm{.}}\hfill & \hfill {\displaystyle \left(20\right)}\end{array}}}\end{array}$ A forgómozgás alapegyenlete a tömegközéppontra $\begin{array}{c}{\displaystyle -\left(S\cdot R+K\cdot \frac{R}{2}\right)=\frac{3}{2}m{R}^2\cdot \beta \mathrm{.}}\end{array}$ (21) Az $a_1$, $a_2$, $\beta$, ${\omega }_2$ mennyiségek nem függetlenek, közöttük az teremt kapcsolatot, hogy tudjuk: az abroncs középpontja függőlegesen nem gyorsul, a vízszintes gyorsulása pedig $R\beta$. $\begin{array}{c}{\displaystyle a_2-\frac{R}{2}\beta =\mathrm{0,}\text{illetve}{a}_1-\frac{R}{2}{\omega }_2^2=R\beta \mathrm{.}}\end{array}$ (22) A (18)‐(22) egyenletekből a nyomóerőre $\begin{array}{c}{\displaystyle K=\frac{15}{8}mg-\frac{m{v}_0^2}{8R}}\end{array}$ adódik, összhangban az I. megoldás (14) képletével. Hasonlóan számíthatók ki az a) kérdésben szereplő helyzetben is az abroncsra ható erők.  Lovász Mónika (Pécs, Nagy L. Gimn., III. 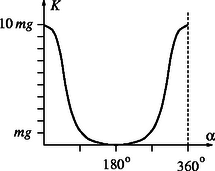o.t.)   Megjegyzések. 1. Felmerül a kérdés, hogy ha a kezdősebességet éppen a (6) feltételnek megfelelő határesetnek választjuk ($v_0=\sqrt[]{8Rg}$, vagyis az abroncs a nehezék legfelső helyzetében nem emelkedik fel), akkor biztosak lehetünk-e benne, hogy a $K$ nyomóerő a mozgás során mindvégig pozitív. Elvben elképzelhető lenne, hogy az abroncs a mozgás korábbi szakaszában valamikor felpattan. Gubás Lóránt László (Miskolc, Földes F. Gimn., III. o.t.) kiszámította, hogy amikor az abroncs középpontját és a nehezéket összekötő egyenes $\alpha$ szöget zár be a függőlegessel, a nyomóerő $\begin{array}{c}{\displaystyle K\left(\alpha \right)=mg\left(\frac{27}{2{\left(2-\text{cos}\alpha \right)}^2}-\text{cos}\alpha -\frac{5}{2}\right)\mathrm{.}}\end{array}$ A nehezék felső helyzeténél $K\left({180}^{\circ }\right)=0$, a b) kérdésbeli esetekben $K\left({90}^{\circ }\right)=K\left({270}^{\circ }\right)=7/8mg$, míg a kezdeti állapotban $K\left(\alpha =0\right)=10mg$. A $K\left(\alpha \right)$ függvény grafikus vizsgálata (8. ábra), illetve függvényanalízis (szélsőérték keresése deriválással) azt igazolja, hogy (6) teljesülése esetén $K\left(\alpha \right)$ sehol nem válik negatívvá. 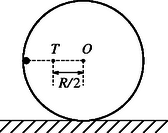2. A nehezék pályája ciklois. Az a) kérdésre sokan úgy próbáltak válaszolni, hogy a nehezék gyorsulását a legfelső helyzetben a $2v_1$ sebességű, $R^{*}$ görbületi sugarú körmozgásból számolták. Úgy érveltek, hogy az abroncs pillanatnyi forgáscentruma a talajjal érintkező pont, tehát $R^{*}=2R$, $a_{\text{nehezék}}=\frac{4v_1^2}{2R}$, s az $mg+mg=m\cdot a_{\text{nehezék}}$ egyenletből $v_1^2=Rg$, azaz $v_0^2=5Rg$. Ez azonban hibás! A ciklois görbületi sugara a kérdéses pontban $R^{*}=4R$, a centripetális gyorsulás pedig ${\left(2v_1\right)}^2/\left(4R\right)=v_1^2/R$. Jól látható, a fenti érvelés tarthatatlansága, ha azt az abroncs középpontjára alkalmazzuk. Ez a pont is a talajjal érintkező pont körül fordul el, a pályájának (ami egyenes) mégsem $R$ a görbületi sugara, hanem végtelen!