Feladat:	2907. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely ,  Csendes Balázs ,  Gyöpös Noémi ,  Léka Zoltán
Füzet:	1996/március, 184. oldal		PDF  |  MathML
Témakör(ök):	Egyenesvonalú mozgás lejtőn, Energia homogén gravitációs mezőben, Feladat
Hivatkozás(ok):	Feladatok: 1995/szeptember: 2907. fizika feladat

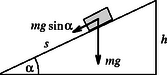
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Egy $s$ hosszúságú, $h$ magasságú lejtő hajlásszögét a $\text{sin}\alpha =h/s$ összefüggésből számíthatjuk ki (lásd az ábrát). Mivel a súrlódásmentesen csúszó testet $mg\text{sin}\alpha$ erő gyorsítja, a gyorsulása $a=gh/s$, az $s$ út megtételéhez szükséges idő pedig $\begin{array}{c}{\displaystyle T=\sqrt[]{\frac{2s}{a}}=s\sqrt[]{\frac{2}{gh}}\mathrm{.}}\end{array}$ Ez a kifejezés | adott $h$ esetén | valóban arányos a lejtő $s$ hosszával, Leonardo da Vincinek tehát igaza volt.   II. megoldás. Az energiamegmaradás tétele szerint egy $h$ magas lejtőről lecsúszó test végsebessége $v=\sqrt[]{2gh}$, az átlagsebessége pedig ennek fele: $v_{\text{átlag}}=\sqrt[]{gh/2}$. Különböző hajlásszögű, de azonos magasságú lejtőknél tehát a mozgás átlagsebessége ugyanakkora, tehát a lejtő hosszának és a mozgás idejének aránya megegyezik. Ez pedig éppen Leonardo da Vinci állítása.  Csendes Balázs (Szekszárd, Garay J. Gimn., II. o.t.)