Kezdőlap


Feladat:	2903. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Németh Tibor , Tóth Gábor Zsolt
Füzet:	1997/február, 103. oldal		PDF \| MathML
Témakör(ök):	Egyéb rögzített tengely körüli forgás, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1995/május: 2903. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rúd tömegközéppontjának vízszintes gyorsulását a súrlódási erő okozza. A tömegközéppont kezdetben ,,előre'' (a dőlés irányába) gyorsul, tehát a súrlódási erőnek is ilyen irányúnak kell lennie. Ha az asztal és a rúd alja közötti tapadási súrlódási együttható nem elég nagy, a rúd alja a dőlés kezdeti szakaszában megcsúszik, méghozzá hátrafelé, a dőlés irányával ellentétesen. Amennyiben ez mégsem következne be, akkor a rúd tömegközéppontja előbb-utóbb lassulni kezd (hiszen a teljes eldőlés pillanatában már nulla lenne a vízszintes irányú sebessége). A lassulást a dőlés irányával ellentétes súrlódási erő okozza, ha tehát a rúd alja a mozgás ezen szakaszában csúszik meg, akkor ezt előrefelé teszi.
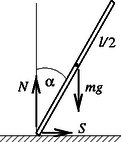
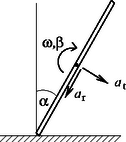
A fentebb leírt kvalitatív kép részletes számítással is nyomon követhető. Az $m$ tömegű, $l$ hosszúságú, a tömegközéppontjára vonatkoztatva $Θ = \frac{1}{12} m l^{2}$ tehetetlenségi nyomatékú rúdra $α$ dőlési szögnél az 1. ábrán látható erők hatnak. Ezek hatására a rúd tömegközéppontja $a_{t}$ érintőleges (tangenciális) és $a_{r}$ sugárirányú (radiális) gyorsulással, továbbá a tömegközéppontja körül $ω$ szögsebességgel és $β$ szöggyorsulással fog mozogni (2. ábra). Mindezek a mennyiségek időben változnak, a mozgás tehát meglehetősen bonyolult.
Felírva a tömegközéppontra vonatkozó (sugár- és érintő irányú) mozgásegyenleteket, a forgómozgás dinamikai egyenletét, az energiamegmaradás tételét, valamint azokat a kényszerfeltételeket, melyek azt fejezik ki, hogy a rúd legalsó pontja a megcsúszás pillanatáig semerre nem gyorsul, kiszámíthatjuk az $N$ nyomóerőt és az $S$ súrlódási erőt az $α$ szög függvényében:

\begin{matrix} \begin{matrix} (1) N = \frac{1}{4} m g {(3 cos α - 1)}^{2}, \\ (2) S = \frac{3}{4} m g sin α (3 cos α - 2) . \end{matrix} \end{matrix}

Látható, hogy az asztal és a rúd közötti nyomóerő kezdetben pozitív, de a dőlés során egyre csökken, s

α_{3} = arc cos \frac{1}{3} = 70, 5^{\circ}

-nál nullává válik. A pálca tehát legkésőbb ennél a szögnél (ténylegesen már ennél hamarabb) megcsúszik.
A megcsúszás akkor következik be, amikor az

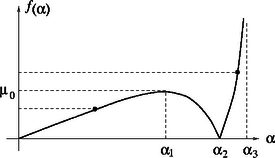
\begin{matrix} f (α) = | \frac{S}{N} | = | \frac{3 sin α (3 cos α - 2)}{{(3 cos α - 1)}^{2}} | \end{matrix}

hányados eléri (vagy meghaladja) a

μ

tapadási súrlódási együttható tényleges értékét. Ábrázolva az

f (α)

függvényt (3. ábra) leolvashatjuk (vagy differenciálszámítás segítségével ki is számíthatjuk), hogy

f (α)

-nak

α_{1} = arc cos \frac{9}{11} \approx 35, 1^{\circ}

-nál lokális maximuma van és

f (α_{1}) = μ_{0} \approx 0, 37.

Amennyiben

μ < μ_{0}

, a rúd alja ,,hátrafelé'' csúszik meg az

f (α) = μ

egyenlet gyökének megfelelő (

α < α_{1}

) szögnél. Ha viszont

μ > μ_{0}

, a rúd ,,előrefelé'' csúszik meg.
Hátra van még annak megfontolása, hogy felemelkedhet-e a rúd alsó vége az asztalról. A megcsúszás pillanatáig biztosan nem, hiszen láttuk, hogy az addig érvényes mozgásegyenletek szerint

N \geq 0

. Az energiaviszonyok tanulmányozásával (a helyzeti, mozgási és forgási energia összehasonlításával, ezek között fennálló egyenlőtlenség felírásával) be lehet látni, hogy a rúd alsó vége még akkor sem emelkedhet fel az asztalról, amikor már megcsúszott azon.

Németh Tibor (Győr, Révai M. Gimn., IV. o.t.) és

Tóth Gábor Zsolt (Budapest, Árpád Gimn., III. o.t.) dolgozata alapján