Feladat:	2852. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bárász Mihály ,  Kovács Bertalan ,  Németh Tibor
Füzet:	1995/május, 310. oldal		PDF  |  MathML
Témakör(ök):	Merev test térbeli mozgása, Coriolis-erő, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1994/december: 2852. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a pálcák tömegét $m_1$-gyel és $m_2$-vel! Mivel a tömegeloszlásuk egyenletes, a tömegük arányos a hosszukkal, vagyis a hosszegységre eső tömegük megegyezik: $\begin{array}{c}{\displaystyle \frac{m_1}{l_1}=\frac{m_2}{l_2}=\lambda \mathrm{.}}\end{array}$ (1) A pálcák kétféleképpen zárhatnak be ${45}^{\circ }$-os szöget a függőlegessel: ha párhuzamosak egymással, vagy ha merőlegesek egymásra. Hasonlóan az FF. 2840. feladat megoldásához (lásd lapunk 304. oldalán), ennél a feladatnál is belátható, hogy a megadott feltételeknek csak a merőlegesen elhelyezkedő pálcák felelnek meg. Foglalkozzunk tehát ezzel az esettel! Írjuk le a pálcák ,,mozgását'' az $\omega$ szögsebességgel forgó koordináta-rendszerből nézve! Ebben a rendszerben a pálcák nem mozognak, egyensúlyban vannak, tehát a rájuk ható erők eredője, illetve az erők forgatónyomatékának összege ‐ külön-külön mindkét pálcára ‐ nulla kell legyen. Az erők és a forgatónyomatékok számításánál figyelembe kell vennünk, hogy a forgó koordináta-rendszer nem inerciarendszer, tehát benne a szokásos valódi (más testekkel való kölcsönhatást kifejező) erőkön kívül ún. tehetetlenségi erők is fellépnek. A koordináta-rendszerhez képest álló testeknél csak egyfajta tehetetlenségi erőt kell számításba vennünk: a centrifugális erőt. 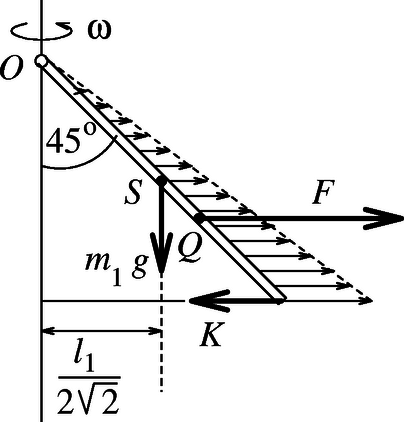A továbbiak könnyebb áttekinthetősége érdekében gondoljuk végig a következő feladatot! Egy $m_1$ tömegű, $l_1$ hosszúságú, homogén tömegeloszlású pálcát, mely ${45}^{\circ }$-os szögben csuklósan csatlakozik a függőleges forgástengelyhez, az alsó végét pedig vízszintes fonál köti össze a tengellyel, $\omega$ szögsebességgel megforgatjuk (1. ábra). Mekkora erő feszíti a fonalat? A forgó koordináta-rendszerből nézve a test az $m_1\text{g}$ nehézségi erő, a $\text{K}$ kötélerő, az $O$ csuklópontnál ható (ismeretlen irányú és nagyságú) erő, valamint a pálca egyes részeire ható centrifugális erők eredőjének hatására egyensúlyban van. Célszerű az $O$ pontra vonatkozó forgatónyomatéki egyenletet felírnunk, mert ebben nem kapnak szerepet az $O$-nál ható erők. (Az erők egyensúlyának feltételét ezek után már nem is érdemes felírni, hiszen ezekből az egyenletekből éppen az $O$-nál ható erőket tudjuk kiszámítani, s ezekre általában nincs szükségünk.) Vajon mekkora a pálca egyes darabkáira ható centrifugális erők eredője? A centrifugális erő helyről helyre változik (a forgástengelytől mért távolság változása miatt), de mivel ez a változás lineáris, az erő nagyságának szempontjából számolhatunk átlagos erővel, vagyis úgy, mintha a test egésze az $S$ tömegközéppontban helyezkedne el: $\begin{array}{c}{\displaystyle F=\sum F_{\text{cf}}=m_1{r}_{\text{átlag}}{\omega }^2=m_1\frac{l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{.}}\end{array}$ Vigyázat: nem szabad azt gondolnunk, hogy ennek az erőnek a támadáspontját is az $S$ pontba helyezhetjük, hiszen a test alsó felére ható centrifugális erők nyilván nagyobbak, mint a felső felére ható erők, s emiatt az $S$ pontra vonatkoztatott eredő forgatónyomatékuk nem nulla. 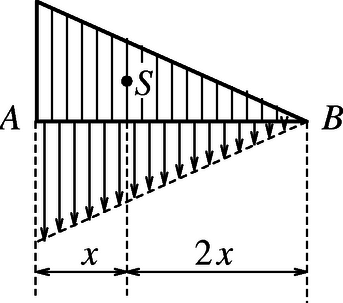Melyik az a $Q$ pont a pálca mentén, amelyre vonatkoztatva a centrifugális erők eredő forgatónyomatéka nulla lenne? Könnyen beláthatjuk, hogy ez a pont a pálca alsó harmadoló pontja. Ha ugyanis egy derékszögű háromszög alakú, homogén anyageloszlású lemezt függőlegesen tartunk úgy, hogy az $AB$ befogó vízszintes legyen (2. ábra), akkor a lemezre ható nehézségi erő is egy lineárisan növekvő erőrendszer eredője, hasonlóan az általunk vizsgált centrifugális erők rendszeréhez. A homogén háromszöglemez tömegközéppontja viszont a háromszög geometriai értelemben vett súlypontjába esik, s ez | mint közismert | harmadolja a súlyvonalakat, függőleges vetülete pedig harmadolja az $AB$ szakaszt. Az 1. ábrán látható pálca egyensúlyának feltétele tehát: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle m_{1}g\frac{l_1}{2\sqrt[]{2}}+K\frac{l_1}{\sqrt[]{2}}=m_1\frac{l_1}{2\sqrt[]{2}}{\omega }^2\cdot \frac{2}{3}\cdot \frac{l_1}{\sqrt[]{2}}\mathrm{,}}\\ \hfill {\displaystyle \text{ahonnan a keresett <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>K</mi></math> kötélerő:}K=m_{1}g\left(\frac{l_1{\omega }^2}{3\sqrt[]{2}g}-\frac{1}{2}\right)\mathrm{.}}\end{array}}}\end{array}$ 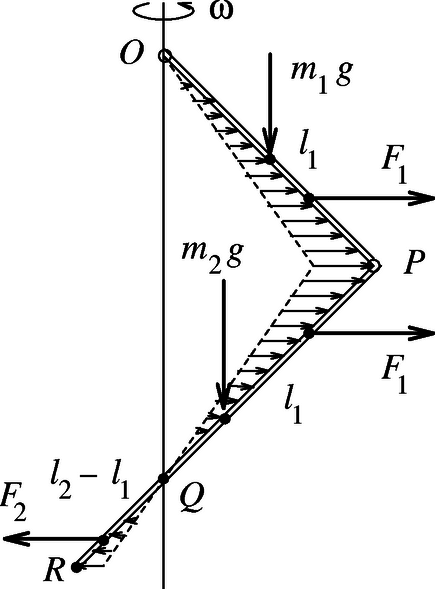Térjünk most vissza az eredeti feladathoz! A felső, $OP$ pálcára $F_1$ centrifugális erő hat, támadáspontja a pálca alsó harmadoló pontja. Az alsó pálca $PQ$ szakaszára ugyancsak $F_1$ erő hat, a $QR$ szakaszra pedig $F_2$, mindkettő a megfelelő szakasz külső (a forgástengelytől távolabb eső) harmadoló pontjánál (3. ábra). A pálcákra hat még a nehézségi erő, amely az egyes pálcák tömegközéppontjában vehető fel, továbbá a $P$ és $O$ csuklópontoknál ismeretlen irányú és ismeretlen nagyságú erők lépnek fel. Ez utóbbiakkal nem kell törődnünk, ha az alsó pálcának a $P$ pontra vonatkozó forgatónyomatéki egyenletét, az egész rendszernek pedig az $O$ pont körüli forgási egyensúly feltételét írjuk fel. Mivel $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(2\right)F_1=m_1\frac{l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{,}}\\ \hfill {\displaystyle \text{és}\left(3\right)F_2=m_2\frac{l_2-l_1}{l_2}\cdot \frac{l_2-l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{,}}\end{array}}}\end{array}$ a $P$ pontra vonatkozó forgási egyensúly feltétele: $\begin{array}{c}{\displaystyle F_1\cdot \frac{l_1}{3\sqrt[]{2}}+m_{2}g\frac{l_2}{2\sqrt[]{2}}=F_2\left(l_2-\frac{l_2-l_1}{3}\right)\frac{1}{\sqrt[]{2}}\mathrm{.}}\end{array}$ (4) Hasonlóan kapjuk a két pálcából álló teljes rendszer $O$ pontra vonatkoztatott forgási egyensúlyi egyenletét: $\begin{array}{c}{\displaystyle m_{1}g\frac{l_1}{2\sqrt[]{2}}+m_{2}g\left(l_2-\frac{l_1}{2}\right)\frac{1}{\sqrt[]{2}}+F_2\left(l_1+l_2-\frac{l_2-l_1}{3}\right)\frac{1}{\sqrt[]{2}}=F_1\left(\frac{2}{3}\frac{l_1}{\sqrt[]{2}}+\frac{4}{3}\frac{l_1}{\sqrt[]{2}}\right)\mathrm{.}}\end{array}$ (5) A (2) és (3) összefüggéseket (4)-be helyettesítve és (1)-t is felhasználva, algebrai átalakítások után $\begin{array}{c}{\displaystyle \sqrt[]{2}g={\omega }^2\left(\frac{2}{3}{l}_2-l_1\right)}\end{array}$ (6) adódik. Ebből ${\omega }^2$-t kifejezve és az (1)-(3) összefüggéseket is felhasználva (5)-be helyettesítés után a $\begin{array}{c}{\displaystyle 7l_2^2-10l_1{l}_2-5l_1^2=0}\end{array}$ (7) egyenletet kapjuk, amely ($l_1^2$-tel osztva) a pálcák hosszának keresett arányára egy másodfokú egyenlet. A számunkra érdekes pozitív gyök $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(8\right)\frac{l_2}{l_1}=\frac{5+\sqrt[]{60}}{7}\approx 1\mathrm{,}\mathrm{82,}}\\ \hfill {\displaystyle \text{s ebből (6) felhasználásával}\omega =\sqrt[]{\frac{3\sqrt[]{2}g}{2l_2-3l_1}}\approx \frac{8\mathrm{,}05}{\sqrt[]{l_1}}\mathrm{,}}\end{array}}}\end{array}$ (amennyiben $l_1$-t méterben mérjük).    Bárász Mihály (Fazekas M. Főv. Gyak. Gimn., III. 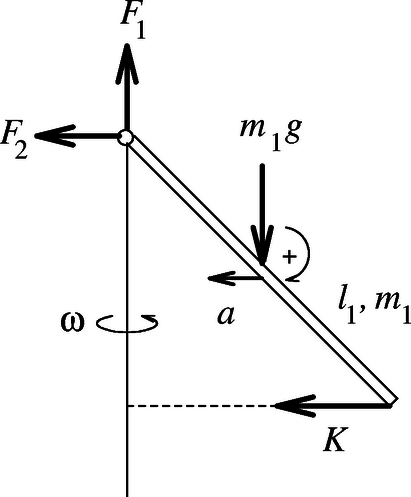o.t.) dolgozata alapján   II. megoldás. Oldjuk meg a feladatot a motorhoz rögzített inerciarendszerben! Ebben a koordináta-rendszerben nem kell számolnunk tehetetlenségi erőkkel, viszont a pálcák (merev testek) mozgásegyenletei bonyolultabbak, mint az egyensúlyi egyenletek. Gyakorlás kedvéért oldjuk meg az I. megoldásban szereplő egyszerűbb feladatot (lásd az 1. ábrát) inerciarendszerből is. Az $m_1$ tömegű, $l_1$ hosszú, $\omega$ szögsebességgel forgó pálca gyorsulása vízszintes irányú, nagysága $\begin{array}{c}{\displaystyle a=\frac{l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{.}}\end{array}$ A pálca mozgásegyenletei, a Newton-egyenletek (a 4. 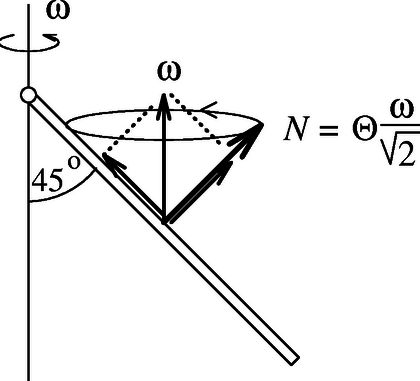ábra jelöléseit követve): $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(9\right)F_2+K=m_1\frac{l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{,}}\\ \hfill {\displaystyle \left(10\right)F_1-m_{1}g=0.}\end{array}}}\end{array}$ A pálcára ható külső erőknek nem nulla a tömegközéppontra vonatkoztatott forgatónyomatéka, hanem (az óramutató járásával megegyező körüljárási irányt tekintve pozitívnak) $\begin{array}{c}{\displaystyle M=\left(F_1-F_2+K\right)\frac{l_1}{2\sqrt[]{2}}}\end{array}$ (11) nagyságú. Célszerű a forgatónyomatékot $\text{M}$ vektornak tekinteni, melynek nagysága $M$, iránya pedig (az erők támadáspontjába mutató helyvektorok és az erők vektoriális szorzatának megfelelően) a papír síkjába befelé mutat. A merev testek forgómozgásának alapegyenlete: $\begin{array}{c}{\displaystyle \text{M}=\frac{\Delta \text{N}}{\Delta t}\mathrm{,}}\end{array}$ (12) ahol $\text{N}$ a merev test perdületének (más néven impulzusnyomatékának) vektora, s a fenti egyenlet jobb oldalán ezen vektor változási sebessége (egységnyi idő alatti megváltozása) szerepel. Hogyan lehet kiszámítani egy test perdületét? Tudjuk, hogy az egész test $\omega$ szögsebességgel forog egy függőleges tengely körül, tehát a tömegközéppontja körüli forgását is egy (függőlegesen felfelé mutató) $\omega$ vektorral jellemezhető. A merev testek perdülete bizonyos esetekben (bizonyos irányú szögsebeségnél) olyan vektor, amely párhuzamos a szögsebesség vektorával, és a nagysága az $\begin{array}{c}{\displaystyle N=\Theta \omega }\end{array}$ (13) összefüggésből számítható ki. A $\Theta$ tehetetlenségi nyomaték a testre és a forgástengely irányára jellemző mennyiség. Egy $m$ tömegű, $l$ hosszú, $r$ sugarú homogén hengernél például ${\Theta }_1=m{r}^2/2$ a szimmetriatengelyre vonatkoztatva, az erre merőleges tengelyre pedig (ha az átmegy a tömegközépponton): ${\Theta }_2=m\left(l^2+3r^2\right)/12$. Vékony, hosszú pálcáknál, amilyen a feladatunkban is szerepel, $r\ll l$ miatt ${\Theta }_1\ll {\Theta }_2\approx m{l}^2/12$. Jelen esetben a szögsebesség vektora se nem párhuzamos a pálca szimmetriatengelyével, se nem merőleges arra, hanem mindkettővel ${45}^{\circ }$-os szöget zár be. Milyen irányú és milyen nagyságú ilyenkor a perdületvektor? Bontsuk fel a szögsebességet a 5. ábrán látható módon két összetevőre. A pálcára merőleges komponens nagysága $\omega /\sqrt[]{2}$, az ennek megfelelő perdület tehát $\begin{array}{c}{\displaystyle N={\Theta }_2\frac{\omega }{\sqrt[]{2}}\mathrm{.}}\end{array}$ (14) A másik szögsebesség-komponens elhanyagolhatóan kicsiny tehetetlenségi nyomatékkal szorzódik, tehát ahhoz nem társítható számottevő nagyságú perdület. Az eredő impulzusnyomaték vektor tehát minden pillanatban merőleges a pálca szimmetriatengelyére, s emiatt a pálcával együtt $\omega$ szögsebességgel forog egy függőleges tengely körül. (Vegyük észre, hogy N iránya most nem párhuzamos a szögsebesség vektor irányával!) Mivel a perdület vektora egy $N/\sqrt[]{2}$ sugarú vízszintes kör mentén $\omega$ szögsebességgel forog, az egységnyi időre eső megváltozása $\begin{array}{c}{\displaystyle \left|\frac{\Delta \text{N}}{\Delta t}\right|=\frac{N}{\sqrt[]{2}}\cdot \omega =\frac{{\Theta }_2{\omega }^2}{2}=\frac{1}{12}{m}_1{l}^2\cdot \frac{{\omega }^2}{2}\mathrm{,}}\end{array}$ (15) iránya pedig az ábra síkjába befele mutat. A pálca forgásának egyenlete tehát (11) és (12) felhasználásával: $\begin{array}{c}{\displaystyle \left(F_1-F_2+K\right)\frac{l_1}{2\sqrt[]{2}}=\frac{1}{24}{m}_1{l}^2\cdot {\omega }^2\mathrm{.}}\end{array}$ (16) A (9), (10) és (16) egyenletek már egyértelműen meghatározzák a pálcára ható erőket, s ha például $K$-t kiszámítjuk, éppen az I. megoldásban más módszerrel megkapott formulához jutunk. Megjegyezzük, hogy a fenti eljárás csak akkor alkalmazható, ha a szögsebességet a merev test úgynevezett fő tehetetlenségi tengelyei szerint bontjuk összetevőkre. Ezeket a tengelyeket általában nem könnyű elemi úton megtalálni; szerencsére fennáll az, hogy szimmetrikus tömegeloszlásoknál a főtengelyek a test szimmetriatengelyeivel esnek egybe. Vigyáznunk kell még arra is, hogy a forgási egyenleteinket a tömegközéppontra vonatkoztassuk. Általános tengelyre vonatkozó forgási egyenlet felírása, ha nem kellő körültekintéssel tesszük, könnyen hibás eredményre vezethet (mint arról részletesen írtunk 1993. évi 5. számunkban | A Szerk.). 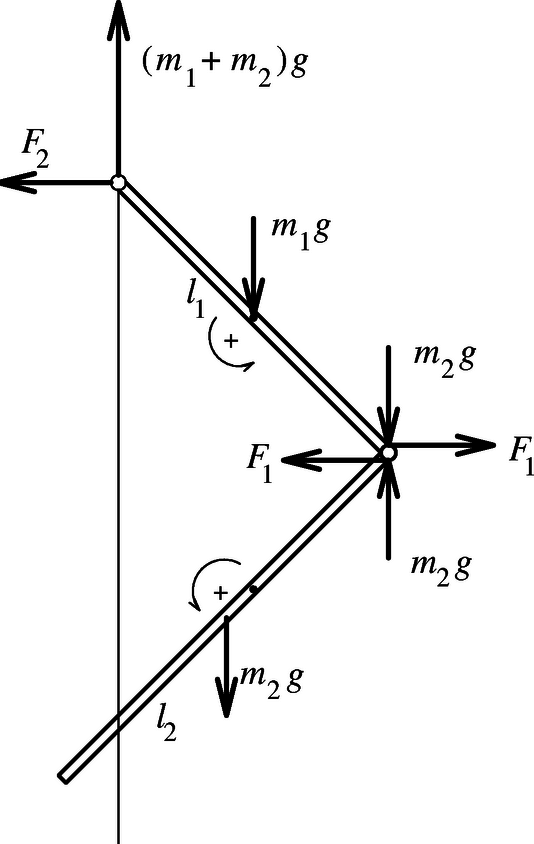Ennyi előtanulmány után már nem túl nehéz a két pálcából álló rendszer mozgásegyenleteinek felírása sem. A 6. ábrán a testekre ható függőleges erőket a függőleges irányú gyorsulás hiányának megfelelően vettük fel. A vízszintes erőket az egyes pálcák tömegközépponti mozgásegyenletéből számíthatjuk ki: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(17\right)F_1=m_2\left(l_1-\frac{l_2}{2}\right)\frac{1}{\sqrt[]{2}}{\omega }^2\mathrm{,}}\\ \hfill {\displaystyle \text{illetve}\left(18\right)F_2-F_1=m_1\frac{l_1}{2\sqrt[]{2}}{\omega }^2\mathrm{.}}\end{array}}}\end{array}$ Ha ezekből kifejezzük $F_1$-t és $F_2$-t, s ezeket a perdületváltozás és a (tömegközéppontokra vonatkoztatott) forgatónyomatékok közötti kapcsolat egyenleteibe helyettesítjük: $\begin{array}{c}{\displaystyle \left(m_{2}g+F_1\right)\frac{l_2}{2\sqrt[]{2}}=\frac{1}{12}{m}_2{l}_2^2\cdot \frac{{\omega }^2}{2}\mathrm{,}}\end{array}$ (19) (a forgatónyomatékok előjelénél figyelembe vettük, hogy a perdület vektorának változása az ábra síkjából kifele mutat), továbbá $\begin{array}{c}{\displaystyle \left(F_1+F_2-m_{1}g-2m_{2}g\right)\frac{l_1}{2\sqrt[]{2}}=\frac{1}{12}{m}_1{l}_1^2\cdot \frac{{\omega }^2}{2}\mathrm{,}}\end{array}$ (20) ahonnan algebrai átalakítások után megkapjuk az I. megoldásban adódott $l_1/l_2$ hosszarányt, illetve a motor fordulatszámát.  Németh Tibor (Győr, Révai M. Gimn., IV. o.t.) dolgozata alapján