Kezdőlap


Feladat:	2502. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Tamás , Csizmadia Péter , Egyedi Péter , Kukorelly Zsolt , Miklós György , Szemlai Ákos
Füzet:	1991/április, 187 - 190. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Feladat
Hivatkozás(ok):	Feladatok: 1990/szeptember: 2502. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rúdra az 1. ábrán látható erők hatnak, ezek hatására a tömegközéppontja gyorsul, s a rúd tömegközéppontja körül elfordul.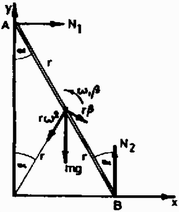

1. ábra

Sem a tömegközéppont gyorsulása, sem pedig a szöggyorsulás nem állandó nagyságú, hanem időben bonyolult módon változó mennyiségek.
A rúd tömegközéppontja ‐ legalábbis a mozgás első szakaszában ‐ egy

r

sugarú körpályán mozog, ahol

r

=1,5 m a rúd félhosszúsága. A rúd szögsebességét

ω

-val, szöggyorsulását

β

-val jelölve a tömegközéppont érintő irányú gyorsulása

r \cdot β

, sugár irányú gyorsulása pedig

r \cdot ω^{2}

.
Célszerű olyan mértékegységrendszert (hosszúság, idő- és tömegegységeket) választanunk, melyben

r = g = m = 1

(

m

a rúd tömege). A számolás végén a dimenziókat figyelve könnyen visszatérhetünk a szokásos SI egységekre.
A rúd tömegközéppontjának mozgásegyenlete az 1. ábra derékszögű koordináta-rendszerében:

\begin{matrix} N_{1} = β \cdot cos α - ω^{2} sin α, \end{matrix}

(1)

\begin{matrix} N_{2} - 1 = - β \cdot sin α - ω^{2} \cdot cos α, \end{matrix}

(2)

a forgómozgás egyenlete pedig

\begin{matrix} N_{2} \cdot sin α - N_{1} \cdot cos α = \frac{1}{3} β . \end{matrix}

(3)

(Ez utóbbi egyenletnél felhasználtuk, hogy a rúd tehetetlenségi nyomatéka

m \cdot {(2 r)}^{2} / 12

a választott mértékegységrendszerben 1/3.)
A rúd szögsebessége az energiamegmaradás törvénye segítségével határozható meg. Mivel a rúd tömegközéppontjának

v = r \cdot ω = ω

sebessége

α = α_{0} = 30^{\circ}

-nál nulla volt, fennáll

\begin{matrix} \frac{1}{2} ω^{2} + \frac{1}{2} \cdot \frac{1}{3} \cdot ω^{2} + cos α = cos α_{0}, \end{matrix}

ahonnan

\begin{matrix} ω^{2} = \frac{3}{2} (cos α_{0} - cos α) . \end{matrix}

(4)

Az (1)‐(4) egyenletekből bármilyen

α

szögre meghatározhatjuk az

N_{1}

N_{2}

ω

és

β

mennyiségek értékét. Például

\begin{matrix} N_{1} = \frac{9}{4} sin α \cdot (cos α - \frac{2}{3} cos α_{0}), \end{matrix}

(5)

továbbá

\begin{matrix} N_{2} = \frac{1}{4} [{(3 cos α - cos α_{0})}^{2} + {sin}^{2} α_{0}] . \end{matrix}

(6)

Látható, hogy míg

N_{2}

tetszőleges

α

esetén pozitív, addig

N_{1}

egy bizonyos

α_{1}

szögnél, amelyre

\begin{matrix} cos α_{1} = \frac{2}{3} cos α_{0}, \end{matrix}

(7)

nullává válik. Ennél a szögnél ‐ melynek numerikus értéke a feladat számadataival

α_{1} =

arccos

1 / \sqrt[]{3} = 54, 7^{\circ}

‐ a rúd elválik a függőleges faltól, s a mozgás további részében

N_{1} \equiv 0.

Az elválás pillanatában a rúd tömegközéppontjának vízszintes sebessége

\begin{matrix} v_{x} = ω (α = α_{1}) \cdot sin α_{1}, \end{matrix}

ami (4) és (7) figyelembe vételével

\begin{matrix} v_{x} = \sqrt[]{\frac{2}{9} {cos}^{3} α_{0}} . \end{matrix}

(8)

Ez a sebesség a mozgás további részében nem változhat meg, hiszen a rúdra már nem hat vízszintes irányú erő.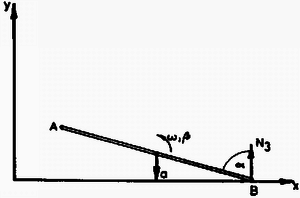

2. ábra

A rúd tömegközéppontja a továbbiakban függőlegesen lefelé gyorsul valamekkora (időben változó)

a

gyorsulással. A mozgásegyenletek a 2. ábra jelöléseivel:

\begin{matrix} N_{3} - 1 & = - a, & (9) \\ N_{3} sin α & = \frac{1}{3} β, & (10) \end{matrix}

az energiamegmaradás tétele pedig az

\begin{matrix} \frac{1}{2} v_{x}^{2} + \frac{1}{2} v^{2} + \frac{1}{2} \cdot \frac{1}{3} \cdot ω^{2} + cos α = cos α_{0} \end{matrix}

(11)

alakot ölti, ahol

v

a tömegközéppont függőleges sebessége. Mivel a rúd alsó végének nincs függőleges sebessége, fenn kell álljon a

\begin{matrix} v - ω \cdot sin α = 0 \end{matrix}

(12)

összefüggés is. Hasonlóan, a rúd végpontjának függőleges gyorsulása is nulla, ahonnan

\begin{matrix} - a + β \cdot sin α + ω^{2} \cdot cos α = 0. \end{matrix}

(13)

Elvben elképzelhető lenne, hogy valamekkora

α

szögnél az

N_{3}

erő nullává válik, vagyis a rúd felemelkedik a talajról. A (9)‐(13) egyenletek azonban azt mutatják, hogy ez mégsem következik be (lásd még a 2422. feladat megoldását az 1990/2 számban).
A földetérés pillanatában

α

= 90

°

, ekkor a tömegközéppont függőleges sebességére

\begin{matrix} v = \sqrt[]{\frac{3}{2} (cos α_{0} - \frac{1}{9} cos^{3} α_{0})}, \end{matrix}

a rúd másik végpontjának teljes sebessége pedig

\begin{matrix} v_{A} = \sqrt[]{v_{x}^{2} + {(2 v)}^{2}} = \sqrt[]{\frac{2}{9} cos^{3} α_{0} + 6 (cos α_{0} - \frac{1}{9} cos^{3} α_{0})} \end{matrix}

adódik. A szokásos SI egységekre úgy térhetünk át, ha a fenti eredményt megszorozzuk

m

r

és

g

-ből képezhető sebesség dimenziójú mennyiséggel,

\sqrt[]{r \cdot g}

-vel, s így végül

\begin{matrix} v_{A} = \sqrt[]{(6 cos α_{0} - \frac{4}{9} cos^{3} α_{0}) r \cdot g} = \sqrt[]{\frac{17 \cdot \sqrt[]{3}}{6} \cdot 1,5 m \cdot 9,81 \frac{m}{s^{2}}} = 8,5 \frac{m}{s} \end{matrix}

adódik. Az

A

pont sebessége a vízszintestől

\begin{matrix} β = arctg \frac{2 v}{v_{x}} = arctg \sqrt[]{3 (\frac{9}{{cos}^{2} α_{0}} - 1)} = arctg \sqrt[]{33} = 80, 1^{\circ} \end{matrix}

szöggel tér el lefelé.

Megjegyzések. 1. Sok megoldó feltételezte, hogy a rúd tömegközéppontja mindvégig körpályán mozog, s az energiamegmaradás törvényéből számolva a lecsapódás sebességére

v_{1} = 8,8 m/s

nagyságú, függőleges irányú vektort kaptak. Ha a tömegközéppont valóban így mozogna, akkor a vízszintes sebessége (amely kezdetben nulla volt) eleinte nőne, majd fokozatosan csökkenve ismét nullává válna. A csökkenő sebesség azonban negatív gyorsulásnak, az pedig negatív vízszintes kényszererőnek felelne meg, s ezt a sima függőleges fal nem képes létrehozni. A feltételezett mozgás más módon, például síneken csúszó csuklókhoz rögzített rúddal megvalósítható.
2. A rúd alsó végpontja nem esik egybe a pillanatnyi forgástengellyel, ezért ezen pontra írva fel a forgómozgás egyenletét ugyancsak hibás eredményt kapunk.
3. A megoldás egyszersmind bemutatja, hogyan lehet ügyes mértékegységrendszer választással egyszerűsíteni a számolást. Aki szerint nem egyszerűbb, hanem furcsább, bonyolultabb lett, az próbálja párhuzamosan, a szokásos egységeket használva, leírni a formulákat, majd vesse össze a két, persze azonos megoldást.