Kezdőlap


Feladat:	2422. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bohus Kálmán , Csonka Gábor , Czibula István , Emődi Sándor , Frohner Ákos , Janszky Imre , Juhász Attila , Pollner Péter , Rácz Andrea , Zóka Gábor
Füzet:	1990/február, 93 - 94. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Nyomóerő, kötélerő, Feladat
Hivatkozás(ok):	Feladatok: 1989/október: 2422. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A mozgás során a rúdra két erő hat: az $m g$ gravitációs erő és az $N$ nyomóerő (1.ábra).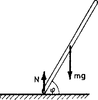

1. ábra

Ha a rúd elválik az asztaltól, akkor az elválás pillanatában a rá ható nyomóerő nulla. Tehát azt kell megvizsgálni, hogy a mozgás folyamán lesz-e olyan pillanat, amikor az

N

nyomóerő nulla.
A rúd mozgása összetehető a tömegközéppont haladó mozgásából és a tömegközéppont körüli forgásból. Legyen a haladó mozgás gyorsulása

a

, a tömegközéppont körüli forgás szöggyorsulása

β

.
A haladó mozgás egyenlete:

\begin{matrix} m g - N = m a, \end{matrix}

(1)

A forgó mozgás egyenlete:

\begin{matrix} N \cdot \frac{L}{2} cos φ = Θ β = f r a c 112 m L^{2} β, \end{matrix}

(2)

ahol

L

a rúd hossza,

Θ

a tömegközéppontra vonatkoztatott tehetetlenségi momentuma.
Mivel nincs súrlódás, mechanikai energia nem vész el. Legyen

v

a haladó mozgás sebessége,

ω

pedig a középpont körüli forgás szögsebessége (2. ábra).

2. ábra

Ekkor az energiaegyenlet:

\begin{matrix} m g \frac{L}{2} (1 - sin φ) = \frac{1}{2} m v^{2} + \frac{1}{2} Θ ω^{2} = \frac{1}{2} m v^{2} + \frac{1}{24} m L^{2} ω^{2} . \end{matrix}

(3)

Amíg a rúd nem válik el az asztaltól, addig az asztallal érintkező pontjának csak vízszintes sebessége és gyorsulása lehet. A sebessége egyrészt a haladó mozgás

v

sebessége lefelé, másrészt a tömegközéppont körüli forgás kerületi sebessége a rúdra merőlegesen. Mivel az eredő függőleges komponense nulla, ezért

\begin{matrix} v = ω \frac{L}{2} cos φ . \end{matrix}

(4)

A rúd asztallal érintkező pontjának gyorsulása a haladó mozgás

a

gyorsulása lefelé, a rúdirányú centripetális gyorsulás és a rúdra merőleges tangenciális gyorsulás (3. ábra).

3. ábra

Mivel az eredő függőleges komponense nulla, ezért

\begin{matrix} ω^{2} \frac{L}{2} sin φ + \frac{L}{2} β cos φ = a . \end{matrix}

(5)

A (3)‐(4) egyenletekből

ω

-t kifejezve:

\begin{matrix} ω^{2} = \frac{g}{L} \frac{12 (1 - sin φ)}{3 cos^{2} φ + 1} . \end{matrix}

(6)

A (2) egyenletből

\begin{matrix} β = \frac{6 N cos φ}{m L} . \end{matrix}

(7)

Az (1) egyenletből

\begin{matrix} a = g - \frac{N}{m} . \end{matrix}

(8)

A (6), (7), (8) egyenleteket (5)-be helyettesítve és rendezve kapjuk, hogy

\begin{matrix} N = m g \frac{3 sin^{2} φ - 6 sin φ + 4}{{(3 cos^{2} φ + 1)}^{2}} . \end{matrix}

(9)

N

akkor válna nullává, ha a számlálóban szereplő kifejezés nulla lenne. Ez

sin φ

-re egy másodfokú egyenlet, amelynek diszkriminánsa negatív, tehát a kifejezés sosem lesz nulla, így

N

sem, tehát a rúd nem válik el az asztaltól.

Csonka Gábor (Budapest, Könyves K. Gimn., III. o. t.)
dolgozata alapján