Kezdőlap


Feladat:	2361. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boncz András , Egyedi Péter , Magyar Gábor
Füzet:	1989/december, 472 - 473. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Tömegpont egyensúlya, Nyomóerő, kötélerő, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1989/január: 2361. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a két tömeg azonos lenne, akkor a szimmetria miatt azonos magasságban helyezkednének el. Most a nagyobb tömeg valamivel mélyebben van. Használjuk az 1. ábra jelöléseit!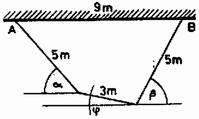

1. ábra

Leolvashatók a következő geometriai összefüggések: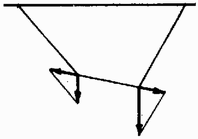

\begin{matrix} 9 = 5 cos α + 3 cos φ + 5 cos β, \\ 5 sin β = 5 sin α + 3 sin φ . \end{matrix}

2. ábra

A súlyerőknek a 3 m-es kötéldarab irányába eső vetületei egyenlőek kell, hogy legyenek (2. ábra). A vetületeket a szinusz-tétel segítségével számolhatjuk ki:

\begin{matrix} 3 \cdot \frac{sin (90 - β)}{sin (β + φ)} = 2 \cdot \frac{sin (90 - α)}{sin (α + φ)} . \end{matrix}

Három egyenletet kaptunk az

α é, é β

φ

ismeretlenekre.
Egyszerű trigonometriai átalakítások után:

\begin{matrix} cos (β + α) = \frac{4}{5} - \frac{27}{25} \cdot cos φ, \\ tg \frac{β - α}{2} = \frac{sin φ}{3 - cos φ}, \\ tg φ = \frac{sin (α + β) - 5 sin (β - α)}{5 \cdot cos (α + β) + 5 \cdot cos (β - α)} . \end{matrix}

(

α + β

) és (

β - α

) szögfüggvényeit az első két egyenletből számíthatjuk, így

φ

-re az alábbi egyenletet kapjuk:

\begin{matrix} tg φ = \frac{\frac{3}{5} \sqrt[]{1 + \frac{24}{5} cos φ - \frac{81}{5} cos^{2} φ} + 5 \cdot \frac{sin φ (3 - cos φ)}{5 - 3 cos φ}}{4 - \frac{27}{5} cos φ + 5 \cdot \frac{9 - 6 cos φ + cos 2 φ}{10 - 6 cos φ}} . \end{matrix}

Az egyenlet numerikusan ‐ táblázat segítségével vagy számítógéppel ‐ megoldható. A feladat szempontjából értelmes egyetlen gyöke

6^{\circ}

és

7^{\circ}

között van, tehát

1^{\circ}

pontossággal igaz, hogy

φ = 6, 5^{\circ}

. A másik két szög hasonló pontossággal

α = 49, 5^{\circ}

β = 56^{\circ}

Boncz András (Zalaegerszeg, Zrínyi M. Gimn., II. o. t.)
dolgozata alapján

Megjegyzés: Az erőkomponensek egyenlőségét ‐ azaz a 3 m-es kötéldarab egyensúlyát ‐ kifejező egyenlet helyett használhattuk volna azt, hogy az adott geometriai feltételek mellett a rendszer helyzeti energiája,

U = - M g l \cdot sin β - m g l sin α

minimális kell, hogy legyen.