Kezdőlap


Feladat:	2334. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1989/március, 140 - 142. oldal		PDF \| MathML
Témakör(ök):	Egyéb változó mozgás, Egyenletes körmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1988/október: 2334. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A dugattyúnak a forgástengelytől mért $x$ távolsága az 1. ábra alapján határozható meg:

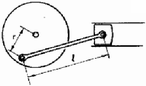1. ábra

\begin{matrix} x = r cos α + l cos β . \end{matrix}

(1)

n

fordulatszámmal működő robbanómotor tengelyének szögsebessége

ω = n π / 30

, a szögelfordulás

α = ω t

. A szinusztétel alapján

\begin{matrix} r sin α = l sin β . \end{matrix}

(2)

Az (1) és (2) egyenletek alapján és

α

helyébe

ω t

-t helyettesítve a következő hely‐idő összefüggést kapjuk:

\begin{matrix} x (t) = r cos (ω t) + \sqrt[]{l^{2} - r^{2} sin^{2} (ω t)} . \end{matrix}

(3)

A sebesség‐idő összefüggés a hely‐idő összefüggés idő szerinti deriváltja, tehát

\begin{matrix} v (t) = x' (t) = - r ω sin (ω t) - \frac{r^{2} ω sin (2 ω t)}{2 \sqrt[]{l^{2} - r^{2} sin^{2} (ω t)}} . \end{matrix}

(4)

A gyorsulás‐idő összefüggés a sebesség‐idő összefüggés idő szerinti deriváltja

\begin{matrix} a (t) = v' (t) = - r ω^{2} cos (ω t) - \frac{r^{2} ω^{2} cos (2 ω t)}{\sqrt[]{l^{2} - r^{2} sin^{2} (ω t)}} - \frac{{[r^{2} ω sin (2 ω t)]}^{2}}{4 {[l^{2} - r^{2} sin^{2} (ω t)]}^{3 / 2}} . \end{matrix}

(5)

II.megoldás. A hely‐idő összefüggést az I. megoldás szerint határozzuk meg. A sebesség kiszámításához keressük meg a hajtókar pillanatnyi forgáscentrumát,

M

-et, azaz azt a pontot, amely körül a hajtókar pillanatnyilag forgómozgást végez. Tudjuk, hogy

M

-ből a hajtókar pontjaiba húzott sugár merőleges az adott pontok sebességeire. A hajtókar

A

pontja

O

körüli körpályán mozog,

B

pontja pedig az

O B

egyenes mentén, ami alapján

M

megszerkeszthető (2. ábra).

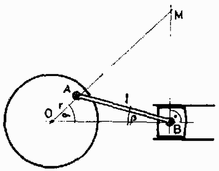2. ábra

Jelölje

ω_{1}

a hajtókar

M

körüli forgásának szögsebességét! Ekkor a dugattyú sebessége, ami a hajtókar

B

pontjának sebességével egyenlő:

\begin{matrix} v (t) = \bar{B M} \cdot ω_{1} . \end{matrix}

(6)

A B M

háromszögre felírt szinusztétel szerint

\begin{matrix} \frac{\bar{A M}}{\bar{B M}} = \frac{cos β}{sin (α + β)}, \end{matrix}

(7)

a hajtókar

A

pontjának sebességéből

\begin{matrix} ω_{1} = \frac{- r ω}{\bar{A M}} . \end{matrix}

(8)

A (6) egyenletbe a (7) és (8) összefüggéseket helyettesítve a (2) összefüggés felhasználásával a sebesség-idő összefüggés I. megoldás szerinti (4) alakját kapjuk.
A gyorsulás‐idő összefüggés meghatározásához a hajtókar mozgását bontsuk fel a jobb oldali végpont mozgására, (amelynek sebessége

v

, gyorsulása

a

), valamint a hajtókar jobb oldali végpontja körüli forgómozgásra. Ez utóbbi forgómozgás szögsebességét jelölje

ω_{2}

, szöggyorsulását

β .

A hajtókar bal oldali végpontjának függőleges sebességét kétféleképpen is felírhatjuk (az

O

, ill. a

B

pontok körüli forgómozgás alapján):

\begin{matrix} r ω cos α = l ω_{2} cos β . \end{matrix}

(9)

Írjuk fel a bal oldali végpont gyorsulásának rúd irányú komponensét is kétféleképpen:

\begin{matrix} r ω^{2} cos [180 - (α + β)] = a cos β + l ω_{2}^{2} . \end{matrix}

(10)

A (9), (10) összefüggésekből némi algebrai átalakítással a gyorsulás‐idő összefüggés már ismert (5) alakja megkapható.

Megjegyzés. Tanulságos vizsgálni az

l ≫ r

esetet. Ekkor közelítőleg

\begin{matrix} x (t) & = r cos ω t - \frac{r^{2}}{2 l} sin^{2} ω t + l, \\ v (t) & = - r ω sin ω t - \frac{r^{2} ω}{2 l} sin 2 ω t, \\ a (t) & = - r ω^{2} cos ω t - \frac{r^{2} ω^{2}}{l} cos 2 ω t, \end{matrix}

azaz megjelennek a kétszeres frekvenciájú felharmonikusok.