Kezdőlap


Feladat:	2325. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Megyeri Gergely
Füzet:	1989/március, 138 - 139. oldal		PDF \| MathML
Témakör(ök):	Tapadó súrlódás, Erők forgatónyomatéka, Feladat
Hivatkozás(ok):	Feladatok: 1988/szeptember: 2325. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a bogár a félgömbhéj valamelyik pontjában áll, akkor ezt tekinthetjük úgy, mintha egy $α$ hajlásszögű lejtőn volna, ahol $α$ a bogár helyén a gömbhéjhoz húzott érintő és a talaj hajlásszöge (1. ábra).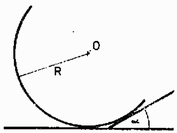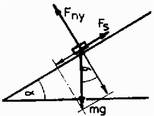

1. ábra

2. ábra

A lejtőknél megismert összefüggés szerint a tapadási súrlódási erőre (2. ábra):

\begin{matrix} F_{s} ≦ μ F_{n y}, \end{matrix}

azaz

\begin{matrix} m g sin α ≦ μ m g cos α . \end{matrix}

\begin{matrix} tg α ≦ μ . \end{matrix}

(1)

A bogár akkor tud kimászni megcsúszás nélkül a labdából, ha mozgása folyamán minden pontban teljesül az (1) feltétel.

3. ábra

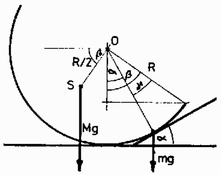A 3. ábra alapján a bogárból és a félgömbhéjból álló rendszerre felírhatjuk a labda középpontjára vonatkozó forgatónyomatékok egyensúlyát:

\begin{matrix} m g R sin α = M g \frac{R}{2} cos β, \end{matrix}

azaz

\begin{matrix} m g R sin (β - γ) = M g \frac{R}{2} cos β, \end{matrix}

(2)

ahol

β

O S

egyenesnek a vízszintessel bezárt szögét,

γ

pedig a bogár helye és a félgömb "szélső'' pontja által meghatározott szöget jelöli

(0 ≦ γ ≦ \frac{π}{2})

.
A (2) összefüggésből

a = \frac{M}{2 m}

jelöléssel

\begin{matrix} \frac{sin (β - γ)}{cos β} = a, \\ tgβcosγ-sinγ= a, tgβ=\frac{a + sin γ}{cos γ}. \end{matrix}

Így

α = β - γ

alapján

\begin{matrix} tg α = \frac{tg β - tg γ}{1 + tg β tg γ} = \frac{a cos γ}{1 + a \cdot sin γ} . \end{matrix}

(3)

Mivel az utóbbi tört számlálója

γ

-nak csökkenő, nevezője pedig

γ

-nak növekvő, pozitív értékű függvénye, ezért

tgαγ

-nak csökkenő függvénye, így

tgα

valamint

α

γ = 0

szélső helyzetben maximális.
Ez azt jelenti, hogy a bogár akkor tud kimászni a labdából, ha még a

γ = 0

szélső helyzetben is teljesül az (1) feltétel, azaz (3) alapján

\begin{matrix} a ≦ μ, \frac{M}{m} ≦ 2 μ = 1, \end{matrix}

vagyis a bogár tömege legalább akkora, mint a labda tömege.

Megyeri Gergely (Bp., Árpád Gimn., III. o. t.)