Kezdőlap


Feladat:	2286. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hauer Tamás , Tóth Ildikó
Füzet:	1989/február, 84 - 86. oldal		PDF \| MathML
Témakör(ök):	Kirchhoff-törvények, Egyéb ellenállás-kapcsolások, Feladat
Hivatkozás(ok):	Feladatok: 1988/január: 2286. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ellenálláshálózatok eredő ellenállásának kiszámításánál nagyon sokat segít, ha megkeressük az ekvipotenciális pontokat. Ezek a pontok ellenállás nélküli vezetékkel összeköthetők, azaz egybeejthetők, így az eredő ellenállás kiszámításához nagyon gyakran nincs szükség másra, mint a sorosan , illetve párhuzamosan kapcsolt ellenállások eredőjének kiszámítására.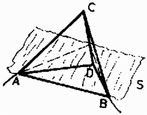
Mivel a szabályos testek minden éle azonos ellenállású, ezért a geometriai szimmetriák a potenciáltérkép szempontjából is léteznek: a testnek az áram be- és kivezetési pontjára (az ábrákon ezeket $A$ és $B$ jelöli) illeszkedő szimmetria síkja azonos potenciálú tükörképi pontokat választ el.

1. ábra

a) Tetraéder esetén (1. ábra) a

C

és

D

pontok tükörképei egymásnak az

A B

-re illeszkedő

S

szimmetriasíkra nézve, így ekvipotenciálisak. A kapcsolást átrajzolva (2. ábra) az eredő ellenállás könnyen kiszámítható: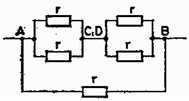

\begin{matrix} R_{tetraéder} = \frac{r}{2} . \end{matrix}

2. ábra

b) Kockánál az

S

szimmetriasík az

A

B

G

és

H

pontokon megy keresztül. Így az

E

és

D

, illetve

F

és

C

pontok ekvipotenciálisak (3. ábra).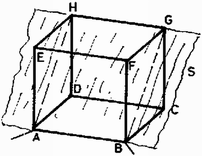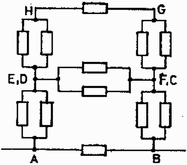

3. ábra

4. ábra

Az átrajzolt hálózat (4. ábra) eredő ellenállása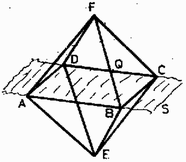

\begin{matrix} R_{kocka} = \frac{7}{12} r . \end{matrix}

5. ábra

c) Oktaédernél a szimmetriasík az

A B C D

sík (5. ábra). Itt

E

és

F

ekvipotenciális. A hálózat rajzánál (6. ábra) figyelembe vettük, hogy a

C D

él

Q

felezőpontja is ekvipotenciális az

E

és

F

pontokkal.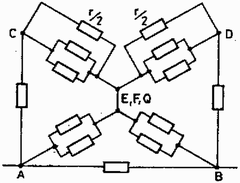

6. ábra

Az eredő ellenállás:

\begin{matrix} R_{oktaéder} = \frac{5}{12} r . \end{matrix}

Hasonló geometriai megfontolások és egyszerű számítások után megkaphatjuk, hogy

\begin{matrix} R_{dodekaéder} = \frac{19}{30} r, \end{matrix}

illetve

\begin{matrix} R_{ikozaéder} = \frac{11}{30} r . \end{matrix}

Tóth Ildikó (Sárvár, Tinódi S. Gimn., III. o. t.)
dolgozata alapján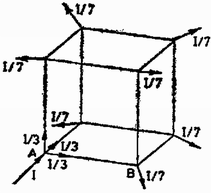

II. megoldás. Valamennyi poliéder esetén egyszerre megadhatjuk a választ, ha kihasználjuk a feladat nagyfokú szimmetriáját, nevezetesen azt, hogy a szabályos poliéderek egyik pontja sincs kitüntetve a többi csúcshoz képest, illetve, hogy mindegyik él ugyanakkora ellenállással rendelkezik.

7. ábra

Jelöljük a csúcsok számát

N

-nel, az egyes csúcsokba futó élek számát

K

-val (kocka esetén pl.

N = 8, K = 3

). Vezessünk a hálózat

A

pontjába

I

erősségű áramot (7. ábra). A többi csúcsból vezessünk el

\frac{I}{N - 1}

erősségű áramot, hogy a töltésmegmaradást kifejező Kirchhoff-törvény teljesüljön. Az

A

ponttal szomszédos csúcsok szimmetrikus szerepe miatt mindegyikük felé

I / K

erősségű áram folyik, így az

A

és

B

pont között a feszültség

\frac{I r}{K}

.
Ismételjük meg az eljárást most oly módon, hogy a

B

pontnál kivezetünk

I

áramot, az összes többi csúcsnál pedig

\frac{I}{N - 1}

áramot vezetünk a hálózatba. Ekkor az

A

és

B

pont között most is

\frac{I r}{K}

lesz a feszültség.

Szuperponáljuk egymásra a két árameloszlást (az Ohm-törvény linearitása miatt ezt megtehetjük). Ekkor az

A

és

B

pontok között

\begin{matrix} U = \frac{I r}{K} + \frac{I r}{K} = \frac{2 I r}{K} \end{matrix}

a feszültség, a teljes átfolyó áramerősség

\begin{matrix} I_{e} = I + \frac{I}{N - 1} = \frac{N}{N - 1} I . \end{matrix}

és a szuperpozíció miatt az

A

és

B

csúcsok kivételével sehol sem folyik ki ‐ vagy be ‐ áram a hálózatba. Így az eredő ellenállás:

\begin{matrix} R = \frac{U}{I_{e}} = \frac{2 (N - 1)}{N \cdot K} r . \end{matrix}

Az öt szabályos poliéderre tehát:

\begin{matrix} N & K & R_{e} \\ tetraéder & 4 & 3 & r / 2, \\ kocka & 8 & 3 & 7 r / 12, \\ oktaéder & 6 & 4 & 5 r / 12, \\ dodekaéder & 20 & 3 & 19 r / 30, \\ ikozaéder & 12 & 5 & 11 r / 30. \end{matrix}

Hauer Tamás (Bp., ELTE Apáczai Csere J. Gimn., IV. o. t.)