Kezdőlap


Feladat:	2262. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bodrogi Péter , Tóth Ildikó
Füzet:	1988/december, 465 - 467. oldal		PDF \| MathML
Témakör(ök):	Gördülés lejtőn, Csúszó súrlódás, Tapadó súrlódás, Energiamegmaradás, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1987/október: 2262. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az abroncs a mozgásának első szakaszában csúszva gördül, majd amikor a súlypontjának sebessége megegyezik a súlypont körüli körmozgásból származó kerületi sebességgel, tiszta gördüléssel mozog tovább.
Legyen az abroncs súlypontjának távolsága a lejtő tetejétől $x$ ! Ekkor a feladatnak megfelelően változó súrlódási együttható:

\begin{matrix} μ (x) = \frac{x}{l}, \end{matrix}

(1)

ahol

l = 1

m, a lejtő teljes hossza.

1. ábra

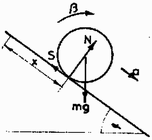Írjuk fel a csúszva gördülés esetén érvényes mozgásegyenleteket! (1. ábra)

\begin{matrix} m g sin α - S = m a, & (2) \\ N = m g cos α, & (3) \\ S R = Θ β, & (4) \end{matrix}

ahol a súrlódási erő:

\begin{matrix} S = μ (x) N, \end{matrix}

(5)

az abroncs tehetetlenségi nyomatéka

\begin{matrix} Θ = m \cdot R^{2}, \end{matrix}

(6)

R

az abroncs sugara,

m

pedig a tömege;

α

a lejtő szöge.
Az (1), (3), (5) és (6) egyenlet segítségével (2) az alábbiakra hozható:

\begin{matrix} a = g sin α - \frac{x}{l} g cos α . \end{matrix}

(7)

Vezessük be az

y = x - l tg α

új változót! (Ez mindössze a koordinátarendszer kezdőpontjának eltolását jelenti, a gyorsulást nem változtatja meg.)
Az új mozgásegyenlet

\begin{matrix} a = - \frac{g cos α}{l} y, \end{matrix}

(8)

amely pontosan olyan alakú (a gyorsulás arányos a ,,kitéréssel'' és vele ellentétes irányú), mint amilyen a harmonikus rezgőmozgásra jellemző. A körfrekvencia (melyet most az abroncs szögsebességétől megkülönböztetve

λ

-val fogunk jelölni):

\begin{matrix} λ = \sqrt[]{\frac{g cos α}{l}} . \end{matrix}

(9)

A rezgőmozgást leíró

y (t)

függvény adatait (paramétereit) úgy kell megválasztanunk, hogy a

t = 0

időpillanatban a sebesség nulla, a kitérés pedig az

x = 0

-nak megfelelő

y = - l tg α

legyen. Ezeknek a feltételeknek

\begin{matrix} y (t) = - l \cdot tg α \cdot cos λ t \end{matrix}

tesz eleget. Az abroncs mozgását leíró (7) egyenlet megoldása tehát

\begin{matrix} x (t) = l tg α (1 - cos λ t), & (10) \\ v (t) = l (tg α) λ sin λ t . & (11) \end{matrix}

A továbbiakban a súlypont körüli forgómozgást vizsgáljuk. A (4)‐(6) és (10) egyenlet alapján:

\begin{matrix} β (t) = \frac{x (t) \cdot g cos α}{l \cdot R} = \frac{g sin α}{R} (1 - cos λ t) . \end{matrix}

(12)

Könnyen belátható, hogy a súlypont körüli forgás szögsebessége:

\begin{matrix} ω (t) = \frac{g sin α}{R} (t - \frac{1}{λ} sin λ t) . \end{matrix}

(13)

(Az

ω (t)

függvény deriváltja éppen a fenti

β (t)

függvényt adja.)
Az eddigi eredmények a csúszva gördülés esetére vonatkoznak. Az abroncs abban a

t_{0}

pillanatban kezd el tisztán gördülni, amikor

v (t_{0}) = ω (t_{0}) \cdot R

.
A (11) és (13) összefüggést felhasználva

t_{0}

-ra adódó egyenlet:

\begin{matrix} 2 sin λ t_{0} = λ t_{0} . \end{matrix}

(14)

Ezt nem lehet elemi úton megoldani, numerikus módszerrel a gyöke:

\begin{matrix} λ t_{0} = η \approx 1,89. \end{matrix}

A fenti gyököt a (10) egyenletbe helyettesítve megkapjuk azt az

x_{0}

távolságot, ahonnan az abroncs tisztán fog gördülni:

\begin{matrix} x_{0} = l tg α (1 + \sqrt[]{1 - {(η / 2)}^{2}}) \approx 1,32 \cdot l \cdot tg α = 0,48 m . \end{matrix}

(15)

Innen a súrlódási erő nem végez munkát az abroncson, így a mozgás során teljesül a mechanikai energiamegmaradás törvénye:

\begin{matrix} \frac{1}{2} m v_{0}^{2} + \frac{1}{2} Θ ω_{0}^{2} + m g (l - x_{0}) sin α = \frac{1}{2} m v^{2} + \frac{1}{2} Θ ω^{2} . \end{matrix}

(16)

Az egyenlet bal oldalának első tagja a haladó mozgás, a második a forgómozgás energiája a tiszta gördülés kezdetén, az utolsó tagja pedig a helyzeti energia megváltozása, amíg a test a lejtő aljára nem ér, ahol a sebessége

v

, szögsebessége

ω

lesz. Mivel tiszta gördülésről van szó, a

v = ω R

feltétel teljesül.

Θ

(6)-beli értékét a (16) egyenletbe írva az abroncs végsebessége:

\begin{matrix} v = \sqrt[]{v_{0}^{2} + g (l - x_{0}) sin α} . \end{matrix}

t_{0}

-beli sebességet a (11) egyenletből kapjuk:

\begin{matrix} v_{0} = l (tg α) λ sin λ t_{0} = \frac{η}{2} {(g l sin α tg α)}^{1 / 2} . \end{matrix}

Ezt behelyettesítve a lejtő alján az abroncs sebessége:

\begin{matrix} v = {g l sin α [1 - tg α (1 - {(η / 2)}^{2} + \sqrt[]{1 - {(η / 2)}^{2}})]}^{1 / 2} \approx \\ \approx {[g l sin α (1 - 0,42 tg α)]}^{1 / 2} = 1,69 m/s . \end{matrix}

Bodrogi Péter (Miskolc, Földes Ferenc Gimn., II. o .t.)

Megjegyzés. Ha felírjuk a tiszta gördülésre vonatkozó mozgásegyenleteket és kényszerfeltételeket, akkor az (1) ‐ (4), (6) egyenletek változatlanul maradnak, az (5) helyébe pedig az

a = β R

kényszerfeltétel kerül. Az egyenletrendszerből

a = \frac{1}{2} g sin α

és

S = m a = \frac{1}{2} m g sin α

; a gördülés feltételeként

μ

-re tehát azt kapjuk, hogy

\frac{1}{2} tg α ≦ μ (x)

, azaz

\begin{matrix} x ≧ \frac{1}{2} tg α = x_{h} . \end{matrix}

A (15) eredmény szerint a tiszta gördülés valójában jóval

x_{h}

után kezdődik, mert a tapadásnak az

S ≦ μ N

egyenlőtlenség csak szükséges, de nem elégséges feltétele. Sok megoldó megfeledkezett erről, és így hibás eredményre jutott.

2. ábra

Ha felrajzoljuk a helyes megoldás segítségével az abroncs sebességének és gyorsulásának idő-függését (2. ábra) (pl. Tóth Ildikó számítógépes programja alapján, vagy a (8), (10) és (11) egyenletekkel analitikusan adjuk meg a görbéket), akkor látható, hogy a gyorsulás-függvénynek a

t_{0}

pontban ugrása van, a hibás eredmény pedig az ábrán berajzolt szaggatott vonalnak a csúszva gördülést meghatározó gyorsulásgörbe

t_{h}

-beli metszéspontja alapján adódik.