Kezdőlap


Feladat:	2252. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csahók Zoltán , Derényi Imre , Láng András , Wolkensdorfer Péter
Füzet:	1988/november, 416 - 417. oldal		PDF \| MathML
Témakör(ök):	Nyomóerő, kötélerő, Egyéb kényszermozgás, Harmonikus rezgőmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1987/szeptember: 2252. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a rendszer helyzetét jellemző változó az 1. ábrán látható 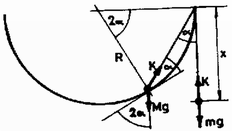$α$ szög.

1. ábra

Határozzuk meg először az egyensúlyi helyzetet megadó

α_{0}

szöget! A fonalat

m g

erő feszíti, ennek érintő irányú összetevője,

m g cos α_{0}

egyensúlyt kell tartson az

M g

súlyerő

M g cos 2 α_{0}

érintőleges komponensével.

\begin{matrix} M g cos 2 α = m g cos α_{0}, \end{matrix}

(1)

ami némi átalakítás után a

\begin{matrix} 2 M cos^{2} α_{0} - m cos α_{0} - M = 0 \end{matrix}

másodfokú egyenletté alakítható. Ennek megoldása

\begin{matrix} cos α_{0} = \frac{m + \sqrt[]{m^{2} + 8 M^{2}}}{4 M}, \end{matrix}

(2)

(a másik gyök a feladat szempontjából érdektelen). Az egyensúly nyilvánvalóan csak úgy állhat fenn, ha

m < M

.
Feladatunk az egyensúlyi helyzet körüli kis amplitúdójú rezgések periódusidejének meghatározása. Térítsük ki a rendszert az egyensúlyi helyzetéből

α = α_{0} + ε

szögnek megfelelő helyzetbe

(ε ≪ 1)

, majd kezdősebesség nélkül engedjük el. Feltevésünk szerint az

α

szög a harmonikus rezgőmozgás képletei szerint váltakozik

T = 2 π / ω

periódusidővel:

\begin{matrix} α = α_{0} + ε cos ω t . \end{matrix}

Az egyensúlyi helyzeten való áthaladás pillanatában a legnagyobb az

α

szög változási sebessége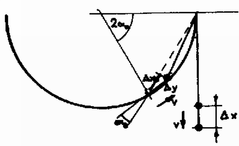

\begin{matrix} {\frac{Δ α}{Δ t} |}_{max} = ε \cdot ω, \end{matrix}

s ezzel együtt a

M

tömegű test

V = R \frac{Δ (2 α)}{Δ t}

sebessége is akkor a legnagyobb,

\begin{matrix} V_{max} = 2 R ω \cdot ε . \end{matrix}

2. ábra

m

tömegű test sebessége a 2. ábra szerint az egyensúlyi helyzet közelében

\begin{matrix} v = \frac{Δ x}{Δ t} = \frac{Δ y \cdot cos α}{Δ t} = V_{max} \cdot cos α_{0} = 2 R ω ε cos α_{0} . \end{matrix}

A rendszer teljes mozgási energiája az egyensúlyi helyzeten való áthaladás pillanatában

\begin{matrix} E_{mozg} = \frac{1}{2} M {(2 R ω ε)}^{2} + \frac{1}{2} m {(2 R ω ε cos α_{0})}^{2} . \end{matrix}

(3)

Számítsuk most ki a rendszer helyzeti energiáját a legnagyobb kitérésnél; az energia nullpontját az egyensúlyi helyzethez rögzítjük. Mivel a

m

tömegű test emelkedése a fonál nyújthatatlansága miatt

\begin{matrix} Δ x = 2 R [sin (α_{0} + ε) - sin α_{0}], \end{matrix}

a helyzeti energia

\begin{matrix} E_{helyz} = m g \cdot 2 R [sin (α_{0} + ε) - sin α_{0}] - & (4) \\ - M g R [sin 2 (α_{0} + ε) - sin 2 α_{0}] . \end{matrix}

Mivel a súrlódás elhanyagolható, a legnagyobb kitéréshez tartozó helyzeti energiának meg kell egyeznie az egyensúlyi helyzeten való áthaladás pillanatában észlelhető maximális mozgási energiával. (3) és (4) összevetéséből

\begin{matrix} 2 (M + m cos^{2} α_{0}) R \cdot ω^{2} \cdot ε^{2} = 2 m g [sin (α_{0} + ε) - sin α_{0}] - & (5) \\ - M g [sin (2 α_{0} + 2 ε) - sin 2 α_{0}] . \end{matrix}

A szögletes zárójelben álló kifejezések az addiciós tétel és a kis szögekre érvényes

sin ε \approx ε

összefüggés felhasználásával

\begin{matrix} sin (α_{0} + ε) - sin α_{0} = (cos ε - 1) sin α_{0} + sin ε \cdot cos α_{0} = \\ = - 2 sin^{2} \frac{ε}{2} \cdot sin α_{0} + sin ε \cdot cos α_{0} \approx ε \cdot cos α_{0} - \frac{1}{2} ε^{2} sin α_{0}, \end{matrix}

illetve

\begin{matrix} sin (2 α_{0} + 2 ε_{0}) - sin 2 α_{0} \approx 2 ε cos 2 α_{0} - 2 ε^{2} \cdot sin 2 α_{0} . \end{matrix}

Tekintettel az (1) egyensúlyi feltételre (5) jobb oldalán az

ε

-nal arányos tagok kiesnek, így mindkét oldalt

ε^{2}

-tel végigosztva az

ω

-ból kiszámítható periódusidő:

\begin{matrix} T = 2 π \cdot \sqrt[]{\frac{2 R}{g} \cdot \frac{M + m cos^{2} α_{0}}{2 M sin 2 α - m sin α_{0}}}, \end{matrix}

ahol

\begin{matrix} α_{0} = arc cos (\frac{m + \sqrt[]{m^{2} + 8 M^{2}}}{4 M}) . \end{matrix}

m ≪ M

, akkor

α_{0} \approx 45^{\circ}

és

T = 2 π \sqrt[]{R / g}

R

hosszúságú fonálinga lengésideje. Általában

T

m / M

tömegarány függvényében a 3. ábrán látható módon változik.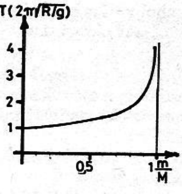

3. ábra

Megjegyzés. Sok megoldó nem vette észre, hogy a két test különböző gyorsulással mozog, és emiatt hibás eredményt kaptak.