Kezdőlap


Feladat:	2251. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csáki Csaba , Czakó Ferenc , Derényi Imre , Láng András , László Ákos , Lévay Ákos , Pásztor Gábor , Szekeres Mária , Wiandt Tamás
Füzet:	1988/november, 413 - 415. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Munkatétel, energiamegmaradás pontrendszerekre, A perdületmegmaradás törvénye, Impulzusváltozás törvénye (Pontrendszer impulzusa), Feladat
Hivatkozás(ok):	Feladatok: 1987/szeptember: 2251. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kövessük végig képzeletben, hogy miként zajlik le a kérdéses ‐ meglehetősen összetett és bonyolult ‐ folyamat. Az érdekesebb helyzetekről készítsünk ábrát is!
a) Ha óvatosan ráhelyeznénk az $m_{1}$ tömegű testet a rugóra, akkor az $Δ x = m_{1} g / D$ hossznyival összenyomódna a nyújtatlan $(n)$ hosszához képest. A rugó ekkor $K = m_{1} g$ erőt fejtene ki mindkét végén. Az emelőre a végein $M g$ , illetve $(m_{1} + m_{2}) g$ nagyságú erő hatna, a forgástengelynél pedig egy megfelelő nagyságú $F$ erő tartana egyensúlyt velük. Mivel az emelő ebben a helyzetben egyensúlyban lenne, a forgatónyomatékok egyensúlya is fenn kell álljon (1. ábra):

\begin{matrix} (m_{1} + m_{2}) g r = M g R . \end{matrix}

(1)

1. ábra

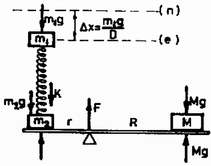Ha a rugót jobban összenyomjuk, minta fentebb tárgyalt egyensúlyi helyzet,

(e)

, akkor az általa kifejtett erő meghaladja az

m_{1} g

értéket, és az emelő egyensúlya megbomlik. Ilyenkor az

m_{2}

tömeg süllyedni kezd, az

M

tömegű test pedig fölfelé gyorsul. Az egyensúlyi helyzetnél hosszabb rugó esetén a helyzet éppen fordított: az

M

tömegű test lefelé gyorsul (illetve kezdetben az alátámasztás miatt egyensúlyban van).
b) Vizsgáljuk ezek után az ütközés egyes fázisait! Az

m_{1}

tömegű testet

h

magasságból leejtve az

\begin{matrix} v_{0} = \sqrt[]{2 g h} \end{matrix}

(2)

sebességgel csapódik a rugó végének (2. ábra).

2. ábra

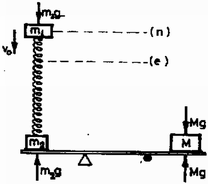A rugó ekkor még feszültségmentes, majd ahogy az

m_{1}

tömegű test lefelé mozog, egyre nagyobb erő ébred benne. Az a) pontban leírtak értelmében az emelő mindaddig nyugalomban marad, míg a rugóerő el nem éri az

m_{1} g

értéket, vagyis amíg a lefelé mozgó (

m_{1}

tömegű) test át nem halad az

(e)

-vel jelzett egyensúlyi helyzeten.
c) Az egyensúlyi helyzeten való áthaladtakor az

m_{1}

tömegű test sebessége

v_{1}

, melynek nagyságát az energia-tételből számíthatjuk ki (3. ábra):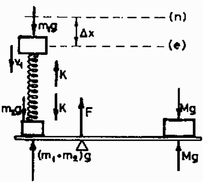

3. ábra

\begin{matrix} \frac{1}{2} m_{1} \cdot v_{0}^{2} + m_{1} \cdot g \cdot \frac{m_{1} \cdot g}{D} = \frac{1}{2} m_{1} \cdot v_{1}^{2} + \frac{1}{2} D \cdot {(\frac{m_{1} \cdot g}{D})}^{2}, \end{matrix}

(3)

ahonnan

\begin{matrix} v_{1} = \sqrt[]{v_{0}^{2} + \frac{m_{1} \cdot g^{2}}{D}} . \end{matrix}

(4)

Ebben a pillanatban az emelő megmozdul, és egyre növekvő szöggyorsulással forogni kezd. A támaszték a továbbiakban nem játszik szerepet, ezért a rajzon föl se tüntetjük.
d) A rugó maximálisan összenyomott állapotában (4. ábra) és még a továbbiakban is az emelő szögsebessége egyre nő, egészen addig, míg az

m_{1}

tömegű test ismét át nem halad az egyensúlyi helyzetnek megfelelő

(e)

vonalon (5. ábra). Feltételezzük, hogy a rugó elég ,,kemény'', emiatt az egész folyamat nagyon gyorsan megy végbe és az emelő szögelfordulása nagyon kicsi. Ez egyúttal azt is jelenti, hogy elhanyagolhatjuk az emelő végpontjainak elmozdulását a 3. és az 5. ábrán látható állapotok közötti időben.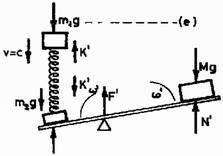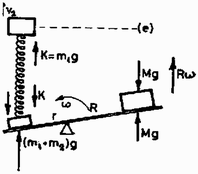

4. ábra

5. ábra

Amikor az

m_{1}

tömeg áthalad az egyensúlyi helyzeten, az emelő valamekkora

ω

szögsebességgel, az

M

tömegű test pedig

R ω

függőleges sebességgel rendelkezik. Mivel a továbbiakban az

M

tömeg már lefelé fog gyorsulni, sebessége egyre csökken, így a keresett legnagyobb függőleges sebesség éppen

R ω

.
Jelöljük az

m_{1}

tömegű test maximális sebességét

v_{2}

-vel, s alkalmazzuk az emelőn levő testek tehetetlenségi nyomatékára a

Θ = m_{2} r^{2} + M R^{2}

jelölést. A

v_{1}

és a

v_{2}

sebességgel jelölt állapotokra (3. és 5. ábra) felírhatjuk az energia és a perdület megmaradásának törvényét. A helyzeti energia változását a folyamat gyorsasága miatt elhanyagoljuk, így

\begin{matrix} \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} m_{1} v_{2}^{2} + \frac{1}{2} Θ ω^{2}, & (5) \\ m_{1} \cdot r (v_{1} + v_{2}) = Θ ω, & (6) \end{matrix}

ahonnan

\begin{matrix} v_{2} = \frac{Θ - m_{1} \cdot r^{2}}{Θ + m_{1} \cdot r^{2}} \cdot v_{1} \end{matrix}

és

\begin{matrix} ω = \frac{2 \cdot m_{1} \cdot r \cdot v_{1}}{Θ + m_{1} \cdot r^{2}} . \end{matrix}

(7)

M

tömegű test sebessége

\begin{matrix} V = R \cdot ω = \frac{2 \cdot m_{1} \cdot v_{1}}{(m_{1} + m_{2}) \frac{r}{R} + M \frac{R}{r}}, \end{matrix}

(8)

ennek keressük a maximumát különböző

r

R

és

M

esetén. Nem szabad azonban megfeledkeznünk arról, hogy ezek a paraméterek nem függetlenek egymástól, hiszen fenn kell állni az (1) egyenlőségnek is. Ebből

M

-t kifejezve és (8)-ba helyettesítve

\begin{matrix} V = \frac{2 \cdot m_{1} \cdot v_{1}}{(m_{1} + m_{2}) (1 + \frac{r}{R})} \end{matrix}

(9)

adódik. Ez a kifejezés akkor maximális, ha a nevező minimális, az pedig az

r / R \to 0

, vagy másképpen írva

R \to \infty

határesetben teljesülne. Azt kaptuk tehát, hogy semmilyen véges

r / R

aránynál nem lehet az

M

tömegű test függőleges "lendülésének'' maximuma. A

V

sebességre csupán egy felső korlátot adhatunk: értéke tetszőlegesen nagy

R

esetén is biztosan kisebb, mint

\begin{matrix} V_{max} = \frac{2 \cdot m_{1}}{m_{1} + m_{2}} v_{1} . \end{matrix}

(Czakó Ferenc)

II. megoldás. Vizsgáljuk a mozgást az egyensúlyi helyzeten való áthaladás pillanatától (3. ábra). Az ütközés első fázisának végén az

m_{1}

és az

m_{2}

tömegű test egy pillanatig egyenlő

c

sebességgel mozog. Jelöljük

F (t)

-vel a pillanatról pillanatra változó nagyságú rugóerőt, és írjuk fel a forgómozgás alapegyenletét, valamint a lendületváltozás tételét:

\begin{matrix} m_{2} g r + F (t) r - M g R = Θ β, & (10) \\ \sum [m_{1} \cdot g - F (t)] Δ t = m_{1} \cdot (c - v_{1}) . & (11) \end{matrix}

(

β

az emelő szöggyorsulását jelöli.) Összegezzük (10)-t az első fázis

t_{1}

idejére:

\begin{matrix} \sum (m_{2} \cdot r - M \cdot R) g \cdot Δ t + r \sum F (t) Δ t = Θ ω = Θ \frac{c}{r} . \end{matrix}

(12)

(11) és (12) összevetéséből

\begin{matrix} (m_{2} g - M g \frac{R}{r} + m_{1} g) t_{1} = m_{1} (c - v_{1}) + Θ \frac{c}{r^{2}} . \end{matrix}

Az egyensúly (1) feltétele miatt a bal oldal nulla, így

\begin{matrix} c = \frac{v_{1}}{1 + \frac{Θ}{m r^{2}}} . \end{matrix}

(13)

Az ütközés második fázisára is felírhatjuk a hasonló egyenleteket, a forgás egyenletét mindjárt összegzett alakban:

\begin{matrix} (m_{2} g r - M g R) t_{2} + \sum F (t) \cdot r \cdot Δ t = Θ (ω - ω') . \end{matrix}

(14)

Kihasználva, hogy egy ideális rugónál

t_{1} = t_{2}

, (14)-ből és (11)-ből, valamint az (1) egyensúlyi feltételből az

M

tömegű test sebességére

\begin{matrix} V = R \cdot ω = \frac{2 m_{1} \cdot v_{1} \cdot R \cdot r}{(m_{1} + m_{2}) r^{2} + M R^{2}} \end{matrix}

adódik. A diszkusszió további része megyezik az I. megoldáséval.
(Wiedemann László)