Kezdőlap


Feladat:	2240. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Csáki Csaba , Hauer Tamás , Horváth András
Füzet:	1988/április, 183 - 184. oldal		PDF \| MathML
Témakör(ök):	Fénytörés, Feladat
Hivatkozás(ok):	Feladatok: 1987/május: 2240. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyezzük a fényforrást az $O z$ tengely egy rögzített $S$ pontjába! Tekintsünk egy fénysugarat, amelyik az $A$ pontban lép a félgömbbe! Ez a pont jellemezhető az 1. ábrán látható 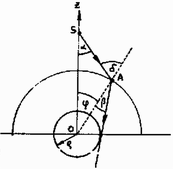$φ$ szöggel.

1. ábra

δ

beesési szög

\begin{matrix} δ = φ + α . \end{matrix}

A törési törvényből

\begin{matrix} \frac{sin δ}{sin β} = n . \end{matrix}

Ez a fénysugár érinteni fogja az

O

középpontú,

ϱ = R sin β

sugarú kört.
Tekintsünk most két fénysugarat (2. ábra)!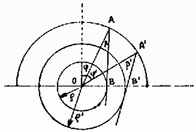

2. ábra

φ < φ'

, akkor

α < α'

és így

δ < δ'

. Ekkor a törési törvényből

β < β'

következik. A második fénysugár így nagyobb

ϱ' = R sin β'

sugarú kört érint. Ez esetben az

A B

és

A' B'

nem metszheti egymást a félgömb belsejében, amiből rögtön következik, hogy

O B < < O B'

.
Következésképpen rögzített

S

mellett

φ

-t a lehető legnagyobbra kell választani. Ez akkor teljesül, ha az

S

-ből induló fénysugár éppen érinti a félgömböt. Ez esetben

\begin{matrix} δ = 90^{\circ}; \end{matrix}

(1)

valamint a törési törvény alapján

\begin{matrix} sin β = \frac{1}{n} . \end{matrix}

(2)

Írjuk fel a szinusztételt az

O B A

háromszögre!

\begin{matrix} \frac{O B}{R} = \frac{sin β}{sin [180 - β - (90 - φ)]} = \frac{sin β}{cos (β - φ)} . \end{matrix}

(3)

Ez az összefüggés adja meg, rögzített

S

mellett, az alaplapon megvilágított kör

O B

sugarát.
Ha azt vizsgáljuk, hogy

O B

mely helyzetű

S

pont esetén lesz minimális, akkor ez megfelel annak, ha

φ

-t változtatjuk

δ = 90^{\circ}

mellett. (3) alapján

O B

minimális, ha

cos (β - φ)

maximális, vagyis

β = φ

. Innen rögtön adódik (2) felhasználásával, hogy:

\begin{matrix} O B = R sin β = \frac{R}{n} . \end{matrix}

(4)

A fényforrás helyzete

β = φ, δ = 90^{\circ}

esetén:

\begin{matrix} O S = \frac{R}{cos α} = \frac{R}{cos β} = \frac{r}{\sqrt[]{1 - sin^{2} β}} = \frac{R n}{\sqrt[]{n^{2} - 1}} . \end{matrix}

(5)

Összefoglalva: Az alaplapon lévő kör területe minimális, ha

O S

az (5)-nek megfelelő érték, a keresett terület pedig:

\begin{matrix} T_{min} = \frac{R^{2} \cdot π}{n^{2}} . \end{matrix}