Feladat: 2224. fizika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Antos András ,  Benczúr Péter ,  Fazekas Anna ,  Lám Judit ,  Petri Zoltán 
Füzet: 1988/március, 135 - 136. oldal  PDF  |  MathML 
Témakör(ök): Ideális gáz állapotegyenlete, Gázok egyéb állapotváltozása, Feladat
Hivatkozás(ok):Feladatok: 1987/április: 2224. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen p0 és V0 a kezdeti nyomás és térfogat, p1 és V1 pedig a végső.

 
 
a)
 

 
 
b)
 

A gáz a legmagasabb hőmérsékletet vagy a folyamat végén (a), vagy pedig a folyamat valamelyik közbenső pontjában (b) éri el. Azt, hogy a jelen esetben melyik eshetőség áll fenn, az 1000  K-es izoterma p0, V0 koordinátájú érintőjének vizsgálatából dönthetjük el. Ha az érintési ponthoz tartozó nyomás kisebb, mint p1, akkora b) eset teljesül, egyébként pedig az a).
Az AB szakasz egy tetszőleges pontjához tartozó nyomás
p=α⋅ΔV+p0,
ahol
ΔV=V0-V1,α=p1-p0V0-V1.
Ezt a pV=n⋅R⋅T gáztörvénybe helyettesítve V-re egy másodfokú egyenletet kapunk:
αV0⋅V+p0⋅V-α⋅V2=n⋅R⋅T.(1)
Ennek az egyenletnek T=1000  K esetén csak egy megoldása lehet (hiszen az egyenes érinti az izotermát), a diszkrimináns tehát nulla kell legyen:
(αV0+p0)2-4αnRT=0.(2)
V0-t a gáztörvényből kaphatjuk meg:
V0=n⋅R⋅T0p0=mM⋅R⋅T0P0=0,227  m3.
Ezt és a többi adatot (2)-be helyettesítve α-ra két megoldást kapunk:
α1=5,5⋅106  Pa/m3,α2=3,5⋅104  Pa/m3,
ami nem meglepő, hiszen az adott izotermához két érintőt is húzhatunk a p0, V0 pontból (c ábra).
 
 
c)
 


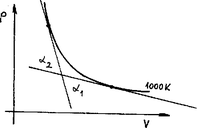A két megoldás közül nekünk nyilván a meredekebbre van szükségünk, mert az tartozik az össznyomáshoz, a másiknál tágítani kellene a gázt ahhoz, hogy a p0 nyomásról elindulva az 1000  K-es izotermát elérhessük. Ezt az α értéket (1)-be visszahelyettesítve és azt V-re megoldva, majd ebből az érintési ponthoz tartozó nyomást kiszámítva 1,8⋅105  Pa, tehát p1-nél kisebb érték adódik. Ezek szerint tehát a b) eset áll fenn.
A végső térfogat:
V1=V0-p1-p0α1=0,063  m3.

 
Megjegyzések. 1. A rossz megoldások többsége azért hibás, mert feltételezi, hogy a gáz a folyamat végén éri el a legmagasabb hőmérsékletet.
2. A jó eredményt kiszámítók közül néhányan úgy szűrték ki a feladat szempontjából érdektelen α2-es meredekségű egyenest, hogy észrevették: az V1-re negatív számot adna! Ez az érvelés a feladat számadatai mellett tényleg alkalmazható, de azért legyünk óvatosak vele. Meg lehetne adni ugyanis olyan adatokat, melyekkel α2 is pozitív V1-re vezetne, de mégsem lenne helyes a megoldás, hiszen az egyenes nem az AB szakasz belsejében érintené az 1000  K-es izotermát, így a gáz a folyamat során egyáltalán nem melegedne föl erre hőmérsékletre.