Kezdőlap


Feladat:	2194. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1987/december, 473 - 476. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Feladat
Hivatkozás(ok):	Feladatok: 1987/január: 2194. fizika feladat

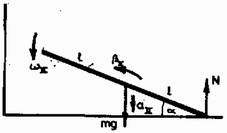
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1. ábrán feltüntettük a vízszintessel $α$ szöget bezáró rúdra, valamint a vízszintesen csúszó tömegpontra ható erőket. A rúd tömegközéppontja egy $l = \frac{L}{2}$ sugarú, $A$ középpontú körpályán mozog.

1. ábra

Jelöljük a tömegközéppont

A

körüli pillanatnyi szögsebességét

ω_{1}

-gyel és a rúdnak a tömegközéppontja körüli szöggyorsulását

β_{1}

-gyel! A szögsebessége a tömegközéppontja körül ugyancsak

ω_{1}

.
Írjuk fel a rúd mozgásegyenleteit! A tömegközéppont gyorsulása és az erők közti kapcsolat:

\begin{matrix} K - F = m (l \cdot β_{1} \cdot sin α - l \end{matrix}

(1)

\begin{matrix} m g - N = (l \cdot ω_{1}^{2} \cdot sin α + l \cdot β_{1} \cdot cos α), \end{matrix}

(2)

ugyanis a tömegközéppont gyorsulása az

l \cdot β_{1}

érintőleges és az

l \cdot ω_{1}^{2}

centripetális gyorsulás eredője.
A vízszintesen mozgó tömegpontra ugyancsak

F

nagyságú erő hat, s ha a gyorsulását

a

-val jelöljük, akkor a mozgásegyenlete

\begin{matrix} F = m \cdot a . \end{matrix}

(3)

A rúd forgását meghatározó egyenlet

\begin{matrix} θ \cdot β_{1} = N \cdot l \cdot cos α - (K + F) \cdot sin α, \end{matrix}

(4)

ahol

\begin{matrix} θ = \frac{1}{12} m {(2 l)}^{2} = \frac{1}{3} m \cdot l^{2} \end{matrix}

a rúd tehetetlenségi nyomatéka a tömegközéppontjára vonatkoztatva.
Mivel a rúd alsó vége érintkezik az

m

tömegű tömegponttal, ennek a pontnak a vízszintes irányú sebessége és a gyorsulása meg kell egyezzék a tömegpont sebességével és gyorsulásával. A rúd alsó végpontjának vízszintes irányú sebessége a tömegközéppont

l \cdot ω_{1}

sebességének

l \cdot ω_{1} \cdot sin α

vízszintes összetevőjéből és a forgómozgásból származó

l \cdot ω_{1}

kerületi sebesség megfelelő vetületéből tehető össze:

\begin{matrix} v = 2 \cdot l \cdot ω_{1} \cdot sin α . \end{matrix}

(5)

Hasonló módon kaphatjuk meg, hogy a rúd alsó végének, s ezzel együtt a tömegpontnak a gyorsulása

\begin{matrix} a = 2 \cdot l \cdot (β_{1} \cdot sin α - ω_{1}^{2} \cdot cos α) . \end{matrix}

(6)

(Az (5) és (6) egyenleteket a differenciálszámítás segítségével is megkaphatjuk, ha képezzük a tömegpont helyét megadó

x = 2 \cdot l \cdot cos α

függvénynek az idő szerinti első, illetve második deriváltját. Figyelem:

Δ α / Δ t = - ω_{1}!)

Használjuk fel a mechanikai energia megmaradásának törvényét is! A helyzeti energia nulla szintjét a talajszinten rögzítve:

\begin{matrix} m \cdot g \cdot l = \frac{1}{2} \cdot \frac{4}{3} m \cdot l^{2} \cdot ω_{1}^{2} + \frac{1}{2} m \cdot {(2 \cdot l \cdot ω_{1} sin α)}^{2} + m \cdot g \cdot l \cdot sin α . \end{matrix}

(7)

A fenti egyenlet jobb oldalának első tagja a rúd teljes mozgási energiája, a második tag pedig a tömegpont energiája.
Az (1)‐(7) egyenletrendszer segítségével tetszőleges

α

szögre kiszámíthatjuk az

F

K

N

erőket, valamint a

v

a

ω_{1}

és

β_{1}

mennyiségeket. Ez a megoldás azonban nem alkalmas a rendszer mozgásának teljes leírására, hanem csak addig érvényes, amíg az

F

K

és

N

erők mindegyike pozitív. (Negatív erő húzásnak felelne meg, s erre sem a fal, sem pedig a talaj nem képes!)
Az (1), (3) és (6) egyenleteket összevetve leolvashatjuk, hogy minden pillanatban fennáll a

\begin{matrix} K = \frac{3}{2} F \end{matrix}

összefüggés, ami azt jelenti, hogy ha valamikor megszűnik a rúd és a fal közti nyomóerő, ugyanabban a pillanatban a rúd és a tömegpont közötti erő is nullává válik. (Részletesebb diszkusszió azt mutatja, hogy

N

a mozgás során mindvégig pozitív marad, vagyis a rúd alsó vége nem emelkedik fel a talajról.)

Határozzuk meg, hogy a rúd milyen helyzeténél válhat

K

és

F

nullává! Az

(1) - (7)

egyenletekből

N

ω_{1}

β_{1}

v

és

a

kiküszöbölése után végül

α

-ra kapunk egy egyenletet:

\begin{matrix} 3 {sin}^{3} α + 3 sin α - 2 = 0. \end{matrix}

(8)

Ezt az egyenletet próbálgatással, vagy grafikusan megoldva az

α_{0}

gyökre

\begin{matrix} sin α_{0} = 0,523 azaz α_{0} = 31, 6^{\circ} \end{matrix}

adódik. Ennél a szögnél a rúd elválik a függőleges faltól, s a tömegpont is elszakad a rúdtól. Mivel a továbbiakban vízszintes irányú erők nem hatnak, mindkét test megtartja az elszakadás pillanatához tartozó vízszintes irányú sebességét (a rúdnál ez természetesen a tömegközéppontra vonatkozik). Elvileg elképzelhető lenne, hogy egy későbbi időpontban a rúd felső vége nekiütközik a falnak, vagy az alsó vége utoléri a tömegpontot, de a részletesebb vizsgálat azt mutatja, hogy ezek egyike sem következik be. Az egyenletrendszer megoldásából a numerikus adatok behelyettesítése után

v = 2,05 m/s

érték adódik; ekkora sebességgel távozik jobb felé a kis test.

2. ábra

A rúd további mozgását a 2. ábrán látható erők szabják meg. A rúd szöggyorsulását

β_{I I}

-vel, tömegközéppontjának függőleges gyorsulását pedig

a_{I I}

-vel jelölve a mozgásegyenletek:

\begin{matrix} m \cdot g - N = m \cdot a_{I I}, \end{matrix}

(9)

\begin{matrix} N \cdot l \cdot cos α = θ β_{I I}, \end{matrix}

(10)

s ehhez járul még egy kényszerfeltétel, amelyik azt fejezi ki, hogy a rúd alsó végpontjának függőleges gyorsulása nulla:

\begin{matrix} a_{I I} = l \cdot β_{I I} \cdot cos α + l \cdot ω_{I I}^{2} \cdot sin α . \end{matrix}

(11)

A rúd szögsebességét ismét az energia-tétel segítségével számíthatjuk ki:

\begin{matrix} m \cdot g \cdot l \cdot sin α + \frac{1}{2} (\frac{1}{3} m \cdot l^{2}) \cdot ω_{I I}^{2} + \frac{1}{2} m \cdot {(l \cdot ω_{I I} cos α)}^{2} = & (12) \\ = m g l \cdot sin α_{0} + \frac{1}{2} (\frac{1}{3} m l^{2}) ω_{0}^{2} + \frac{1}{2} m {(l ω_{0} cos α_{0})}^{2} . \end{matrix}

A bal oldal első tagja a helyzeti energia, a második tag az

ω_{I I}

szögsebességű rúd forgási energiája, a harmadik pedig a függőleges irányú tömegközépponti mozgáshoz rendelhető energia; a jobb oldalon ugyanezeket találjuk a faltól való elszakadás pillanatában. (A vízszintes irányú mozgás energiáját nem szükséges felírnunk, hiszen az időben állandó mennyiség.)
A (9)‐(12) egyenletrendszert megoldva azt találjuk, hogy

N

mindvégig pozitív, tehát a rúd alsó vége nem emelkedik föl a talajról. Ha a mozgás részletesebb leírása helyett csupán arra vagyunk kíváncsiak, hogy mekkora sebességgel érkezik a rúd felső vége a talajhoz, akkor a (12) egyenletből

α = 0

esetén meghatározhatjuk a rúd

ω_{max}

szögsebességét, s ebből a "felső'' vég sebességére

\begin{matrix} v_{max} = 2 \cdot l \cdot ω_{max} = 6,56 m/s \end{matrix}

adódik.