Feladat: 2168. fizika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Cserti József ,  Csordás Zoltán Mihály 
Füzet: 1987/szeptember, 276 - 279. oldal  PDF  |  MathML 
Témakör(ök): Körmozgás (Tömegpont mozgásegyenlete), Tapadó súrlódás, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):Feladatok: 1986/november: 2168. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat szövegéből nem derül ki, hogy hogyan áll a kúp, ,,szájával'' felfelé, vagy pedig lefelé (1. és 2. ábra). A két esetben alapvetően különböző eredményt kapunk, ezért külön-külön vizsgáljuk őket.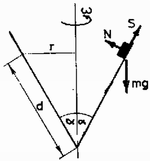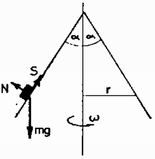

 
 
1. ábra
 

 
 
2. ábra
 

Tekintsük az 1. ábrának megfelelő esetet ! Az ábrán láthatók a testre ható erők. Az r=d⋅sinα sugarú körpályán mozgó test gyorsulása ω2⋅r, iránya a kör középpontja felé mutat. Az m tömegű test mozgásegyenletei: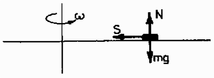
N⋅sinα+S⋅cosα=m⋅g,(1)N⋅cosα-S⋅sinα=m⋅r⋅ω2,(2)S≤μ⋅N.(3)
Az utolsó egyenlet a tapadás feltételét fejezi ki.
 
 
3. ábra
 

Az (1) és (2) egyenletekből N és S kifejezhető, majd ezeket (3)-ba írva a szögsebességre egy egyenlőtlenséget kapunk:
ω≥gr⋅cosα-μ⋅sinαsinα+μ⋅cosα=ω1(α).(4)
A súrlódási erő irányát úgy vettük fel, hogy a testnek a paláston való lecsúszását akadályozza, (4) tehát annak a feltétele, hogy a test ne csúszhasson meg lefelé.
Elképzelhető az is, hogy elegendően nagy ω-nál a test a paláston felfelé kezd el csúszni. Ekkor S iránya az előzőekhez képest ellentétes, tehát az (1) és (2) egyenletekben S helyébe -S írandó. Ismét kifejezhetjük az erőket, s a tapadási feltételből a szögsebességre az
ω≤gr⋅cosα+μ⋅sinαsinα-μ⋅cosα=ω2(α).(5)
megszorítást kapjuk.
Elemezzük a kapott eredményeket ! A (4) egyenlőtlenség azt jelenti, hogy ω≥ω1(α) szögsebességnél a test nem kezd lefelé csúszni, míg (5) szerint ω≤ω2(α) esetén a test nem csúszik felfelé. Másrészt (4) és (5) csak akkor adnak értelmes korlátokat, ha a gyökjel alatt pozitív kifejezés áll, vagyis ha ctgα≥μ és tgα>μ.
Vezessük be az α1=arcctgμ és az α2=arctgμ jelöléseket ! Ha α>α1, akkor ω1(α) nincs értelmezve, másrészt még ω=0-nál sem csúszik le a test. Ugyanakkor ω nem lehet nagyobb ω2(α)-nál, mert különben a test felfelé kicsúsznék a kúpból. A stabil egyensúly feltétele: α>α1 és 0≤ω≤ω2(α).
Ha α<α1(ctgα<μ), akkor ω<ω1(α)-nak kell teljesülnie ahhoz, hogy a test ne csússzék le a kúpon, de a szögsebesség most sem lehet nagyobb ω2(α)-nál. Tegyük fel, hogy α2<α<α1, ekkor létezik ,,kritikus felső szögsebesség'', s az egyensúly feltétele ω1(α)≤ω≤ω2(α).
Ha α<α2, akkor az alsó kritikus érték, ω1(α) értelmezve van, és ω<ω1(α)-nál lecsúszik a test, a felső határ viszont nem létezik, ami annyit jelent, hogy a test felfelé semilyen ω értéknél sem csúszhat meg.
Végül vizsgáljuk meg az α=90∘-os speciális esetet !  Könnyen belátható, hogy S=m⋅d⋅ω2 és N=m⋅g, így ω≤μ⋅gd-nél nem csúszik meg a test.
A fenti eredményeket célszerű egy ,,állapotdiagramon'' szemléltetni. Mérjük fel a vízszintes koordinátatengelyre a kúp szögsebességét, a függőleges tengelyre pedig a félnyílásszögét! Rögzített μ=0,5 és μ=0,1 súrlódási együtthatók mellett felrajzoltuk az ω1(α) ,,alsó kritikus'', illetve az ω2(α) ,,felső kritikus'' szögsebesség görbéjét g/d egységekben. (r helyébe d⋅sinα-t írtunk és a görbék pontjait számítógéppel határoztuk meg.) A diagram segítségével tetszőleges α és ω esetén megállapíthatjuk, hogy a test nyugalomban van-e illetve ha nem, akkor melyik irányba mozdul el (4/a és 4/b ábra).
 
 
4/a ábra
 

 
 
4/b ábra
 

Térjünk át a szájával lefelé álló kúpon levő test stabilitásának vizsgálatára ! Az erőviszonyokat a 2. ábra mutatja. Ismét felírhatjuk a mozgásegyenleteket és a tapadás feltételét:
N⋅sinα+S⋅cosα=m⋅g,(6)-N⋅cosα+S⋅sinα=m⋅r⋅ω2,(7)S≦μ⋅N.(8)
A (6) és (7) egyenletekből N-t kifejezve:
N=m⋅g⋅sinα-m⋅r⋅ω2⋅cosα,(9)
majd a súrlódási erőt is meghatározva és (8)-ba helyettesítve a szögsebességre az
ω≤gr⋅-cosα+μsinαsinα+μcosα=ω3(α)(10)
megszorítást kapjuk. Ha ω=0, akkor μ≥ctgα, vagyis α≥α1 az egyensúly feltétele; ω≠0-nál (de még mindig α>α1-nél) viszont ω≤ω3(α) a stabilitás feltétele.
Amennyiben α<α1, akkor a test már ω=0 értéknél is lecsúszik, tehát semmilyen más szögsebességnél sem lehet egyensúlyban.
Túlságosan nagy ω értéknél az is előfordulhat, hogy N értéke negatívvá válik, ami annyit jelent, hogy a test elválik a kúp palástjától, ,,elszáll''. A (9) összefüggésből kiszámíthatjuk azt a kritikus szögsebességet, amelynél N éppen nullává válik:
ω4(α)=gr⋅tgα.(11)
Ebből látszik, hogy minden α szöghöz tartozik egy felső kritikus szögsebesség, amely fölött a test nem maradhat a kúpon.
A lefelé szélesedő kúpnál is megrajzolhatjuk az állapotdiagramot (5/a és 5/b ábra).
 
 
5/a ábra
 

 
 
5/b ábra
 
(Ismét két különböző súrlódási együtthatóra végeztük el a számítást.) Az ábrákról leolvasható, hogy a súrlódás csökkenésével ,,beszűkül'' a stabil tartomány.
 


Megjegyzés: Teljesen jó megoldás nem érkezett. Több megoldó észrevette, hogy a feladat nincs egyértelműen megfogalmazva, de teljes diszkussziót nem adtak. Azok, akik elkezdték elemezni a különböző eseteket, de hiányos a megoldásuk, 4 pontot kaptak. Akik a fenti esetek valamelyikét vizsgálták csak, 3 pontot szereztek. Sok hibás dolgozat született a centripetális erővel kapcsolatos fogalmi zavarok miatt.