Kezdőlap


Feladat:	2161. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bíró Zoltán
Füzet:	1987/május, 236 - 237. oldal		PDF \| MathML
Témakör(ök):	Rezgőkör, Elektromos töltés megmaradása, Feladat
Hivatkozás(ok):	Feladatok: 1986/október: 2161. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a körben folyó áramot és az egyes kondenzátorlemezeken levő töltést az ábrán látható módon!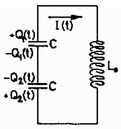

Kezdetben

Q_{1} = q, Q_{2} = 0 és I = 0.

A két kondenzátor közös elektródáján az össztöltés kezdetben

- q,

s ez a későbbiekben sem változhat meg, tehát fenn kell állnia minden pillanatban a

\begin{matrix} Q_{1} (t) + Q_{2} (t) = q \end{matrix}

összefüggésnek.
Az áram irányában haladva a tekercsen, illetve a kondenzátorokon

- L_{0} \frac{d I (t)}{d t}

- \frac{Q_{2} (t)}{C}

és

+ \frac{Q_{1} (t)}{C}

feszültséget mérhetünk; ezek összege Kirchhoff törvénye szerint nulla kell legyen:

\begin{matrix} - L_{0} \frac{d I (t)}{d t} + \frac{Q_{1} - Q_{2}}{C} = 0. \end{matrix}

Kihasználva a töltések közti kapcsolatot, továbbá az

\begin{matrix} I (t) = \frac{d Q_{1} (t)}{d t} \end{matrix}

összefüggést, a

Q_{1} (t)

függvényre a

\begin{matrix} Q_{1} (t) - q / 2 = - \frac{L C}{2} {\ddot{Q}}_{1} (t) \end{matrix}

egyenletet kapjuk (

{\ddot{Q}}_{1}

az idő szerinti második deriváltat jelöli).
Vegyük észre a hasonlóságot a fenti egyenlet és a rezgőmozgás differenciál-egyenlete között! Az analógia alapján (mivel

Q = q / 2

felel meg az egyensúlyi, gyorsulásmentes helyzetnek,

ω = \sqrt[]{2 / (L C)}

pedig a körfrekvenciának) a megoldás:

\begin{matrix} Q_{1} (t) = \frac{q}{2} + A \cdot cos (ω t + φ) . \end{matrix}

A kezdeti feltételek szerint

Q_{1} (0) = q

és

I (0) = 0,

ahonnan a rezgés amplitudójára

A = q / 2,

fázisára pedig

φ = 0

adódik. Így tehát az egyes mennyiségek időfüggése:

\begin{matrix} Q_{1} (t) & = \frac{q}{2} (1 + cos ω t), \\ Q_{2} (t) & = \frac{q}{2} (1 - cos ω t), \\ I (t) & = \frac{q}{2} \cdot ω \cdot sin ω t . \end{matrix}